SPF算法介绍

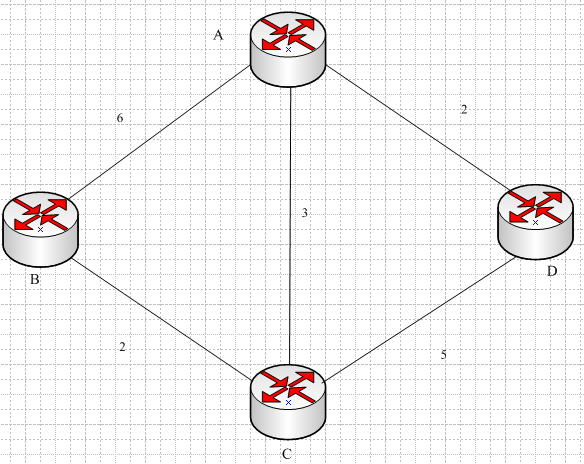
在同步以后，每个路由器的链路状态数据库如下表：

在SPF计算中，每个路由器维护了两个列表：

a.一个在通往目的地的最短路径上的结点列表，这个表也成为路径类表（PATH list）。

b.可能在也可能不在到达目的地的最短路径上的下一跳类表，这个表称为TENTative或TENT列表。

算法如下：

1.把自己列入PATH列表（每台路由器以自己为根结点就是这样由来的），并且距离为0，下一跳也是自己。

2.从PATH列表中取出刚放入的结点，这个结点称为路径结点，查找路径结点的邻居列表，把列表中的每一个邻居加入到TENT列表，下一跳都设置为TENT结点自己，除非该邻居已经在TENT或PATH列表并且代价较小。把加入TENT列表的结点称为TENT结点。把到达TENT结点的代价设为从根结点的代价加上从PATH结点到TENT结点之和。如果加入的结点在TENT列表中已经存在，但是代价较大，就用当前的结点取代代价较高的结点。

3.在TENT列表中找到代价最低的邻居，把邻居加入到PATH列表中，重复第二步。如果TENT列表为空，就停止。

实例：计算上图中路由器A的路由表项。

1.把自己加入PATH列表中，距离为0，下一跳是自己。路由器A的数据库如下表：

2.将邻居B、C和D加入TENT列表中，下一跳为自己。

3.D的代价小于C的3和B的6，将{D,2,D}移到PATH列表中。

4.检查D的邻居。路由D到C的链路代价是5，A-D-C的代价为2+5=7，大于A-C-C的代价3，所以将{C,3,C}加入到PATH列表中：

5.检查C的邻居。路由C到B的链路代价是2，A-C-B的代价为3+2=5，小于A-B-B的代价6，所以在TENT列表中删除{B,6,B}，添加{B,5,C}：

6.将{B,5,C}加入PATH列表，这时A的所有列表已经在PATH列表中了，TENT列表为NULL，停止计算：

7.这时候A的PATH列表就成了它的路由表项：