前面给出的导数定义都依赖于函数极限的概念,我们对极限只做了最简短的解释。现在,我们已经知道了这一概念的目的,接下来关心一下它的意义。
考虑函数
f(x)
,自变量在点
a
的领域内都有定义,但是
L
,当
a
时,
L
(图1)。对于这种情况我们说
x
趋近
f(x)
的极限,用符号表示为
limx→af(x)=L.(1)
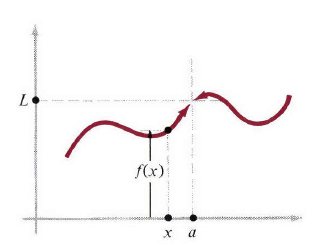
图1
如果不存在这样的实数
L
a
limx→af(x)
f(x)→Lasx→a
现在考虑(1)式的意义,
x
等于
f(x)
会如何是没有意义的;而对于
x
接近
f(x)
值才是有意义的,理解这一点非常重要。
对于(1)式来说,这些非正式的描述对我们直观的理解非常有利,并且对于实际需求也足够了。然而,作为定义,他们又不严谨也不精确,因为有越来越接近和趋近这样的含糊用语。(1)式的精确意义非常重要,所以我们不能只留给学生去想象。我们尽可能简洁又清晰的给出一个令人满意的定义。接下来的部分,阅读的时候最好比平时更仔细些,及饬令他们自然的不耐烦用什么似乎是过度的挑剔的精度。
首先分析一个具体的实例,希望从中可以提取出通用情况的本质
limx→02x2+xx=1
这里我们必须验证的函数是
y=f(x)=2x2+xx
这个函数在
x=0
处无定义,除了
x≠0
外的所有
x
,化简表达式的
从图2中,我们可以清楚的看到,当
x
趋近于
f(x)
趋近于
1
。为了给出定量的描述,我们需要
1
之差的公式:
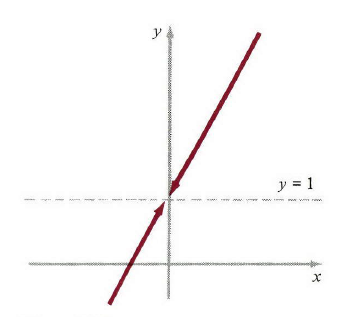
图2
从公式中可以看到
f(x)
1
0