收到启发，昨天闲着没事，回顾了一下关于背包问题的内容，今天是做一个小结，稍晚还有两篇博文。

这篇博文的话，不会有具体的题目，只是对思路进行阐述，需要一定的基础。毕竟博文主要的目的还是给自己当做云笔记使用，如果能够在一定程度帮助他人，那么荣幸之至。

0-1 背包问题

接下来的完全，多重背包问题都是基于这个玩意来进行的。这个点还是非常重要的。

这里我不想做过多的介绍，我们先来聊聊这玩意的状态转移方程。

dp[i][j] = value 这个value 自然是表示在背包容量为j的情况下，拿 i 物体能够达到的最大价值。

对于非常单纯的0-1背包问题，有两个必要的玩意，一个是 C数组，这个C数组在这里表示对应的价值（物品） 还有是 W 数组，表示当前物品的质量，然后当然是咱们的约束了，背包容量是吧。

状态转移方程:

dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+C[i])

降维

由于这个是二维的，所以为了安全（避免溢出）必然是要进行二维数组降为，使用滚动数组的思想。

此时的Dp 方程变成了 这玩意：

dp[j] = max(dp[j-w[i]] + C[i],dp[j])

这个时候，由于我们是要的前一个状态的，我们的每一个物品是只能够最多重复一次的，因为只能拿一次。
如果你是正向从左到右开始填表的话，那么你会发现每一个表示当前最优的，那么最优的可能是选择了物品i,对于下一个选择很有可能还会选择物品i，导致物品i 可能被选择多次。（这个具体的可以自己debug，或者手动走一遍流程）所以，此时要从后面开始遍历。
假设，我是从1开始的。

for(int i=1;i<=n;i++){for(int j=m;j>=1;j--){
		dp[j]=max(dp[j],dp[j-w[i]]+C[i])}}

这里自己注意边界条件判断。

抽象建模

到了这里，随便说了一个那个0-1背包问题，那么接下来是如何判断一个玩意是这个0-1背包问题，这里还是随便简单复述，这几天是得好好和dp有个了解了，如何dp建模是我一直搞不清楚的问题，凭什么别人一眼就能看出这个玩意，并且很快搞出dp方程，而我只能默默地使用“暴力”。我虽然菜，但是不服气呀！！！

这里的话还是聊聊先前一直困扰我的问题，就是质因数拆分的dp。质因数，这个拆分有个特点，就是那些质数只能选择一次，这个和0-1有点像问题是如何联系。

首先 背包问题：

有容量限制

物品有质量

物品有价值

回到质因数拆分。

将 20192019 拆分为若干个两两不同的质数之和，一共有多少种不同的方法？ 注意交换顺序视为同一种方法，例如 2 + 2017 = 20192+2017=2019 与 2017 + 2 = 20192017+2=2019 视为同一种方法。

容量有了，2019
质量有了，我们每一个质数不就是物品，大小不就是质量嘛
价值，问题开始在这里出现歧义了，这里还没确定，我们先不管
我们先看看：

dp 表示
我们翻译翻译，dp[i][j] 原来表示在背包容量为j时，拿第i个物品能够搞到的最大价值
现在表示拿第i个质数，组合j这个数子，能够搞到的组合数量。

因为题目要求是你这个，那么我们当然要的dp的含义也应该是这个，结合0-1的细节。
这个时候我们发现，C数组好像也应该对应的是dp数组。 也就是说，C 表示的实际价值，其实应该是组合数。
（不过在数学上面我一直想不通，虽然在这个0-1模型里面能够解释清楚，不清楚的多理解理解 dp 的含义以及 背包问题 C 数组（价值）的意义）
此时我们好像都确定了，那么对于dp方程的样子是不是还一样？
0-1 的重点，或者背包的重点好像是在，拿和不拿上面，什么情况下，我应该去拿，什么时候我不能去拿？ 以及我拿的时候有什么约束，只能最多拿一个就是0-1背包问题。

那么在这个题目里面，什么情况下拿？还是最大的时候？显然不是呀，我们的C数组都不同了。

如果当前的质数，也就是质量比背包大，肯定不拿，如果小咧，我们还是可以 MAX 拿不拿嘛。
但是，我们可以知道dp表示的一定是最优值，我们只要知道C数组，这个表示的加上这玩意能够达到的组合数，刚好就是dp里面的值，所以此时直接加。

packagecom.huterox.LevelTest2;importjava.util.ArrayList;importjava.util.Scanner;publicclass 质数拆分{staticlong dp[][];staticintW[];publicstaticvoidmain(String[] args){Scanner sc=newScanner(System.in);ArrayList list=newArrayList<Integer>();W=newint[2020];int k=1;//从1开始for(int i=2; i<=2019; i++){if(is(i))W[k++]= i;}
        dp=newlong[2020][2020];
        dp[0][0]=1;//拿0个质数使得和为0，存在这样的的方案1种for(int i=1; i<k; i++){for(int j=0; j<=2019; j++){if(W[i]>j)
                    dp[i][j]= dp[i-1][j];//不选ielse
                    dp[i][j]+= dp[i-1][j-W[i]];}}System.out.println(dp[k-1][2019]);}staticbooleanis(int a){if(a==1||a==0)returnfalse;else{for(int i=2; i<=Math.sqrt(a); i++){if(a%i==0)returnfalse;}returntrue;}}}

完全背包

区别就是物品个数无限制。

我们回到，一开始的0-1背包，我认为这玩意的本质是拿不拿，怎么样拿。

这个时候我们可以拿到多个。所以，理论上可以直接在0-1背包上这样干。

for(int i=1;i<=n;i++){for(int j=m;j>=1;j--){for(int k=0;k<=j/w[i];k++)
			dp[j]=max(dp[j],dp[j-k*w[i]]+k*C[i])}}

这里我写出二维的状态dp

dp[i][j] = max(dp[i-1][j],dp[i][j-w[i]]+C[i])

降维度之后，还是一样的。
然后，还记得为什么0-1要从左到右呢？

所以这里，直接从左到右。此时就是完全背包。

多重背包

这个多重背包是多了约束，那就是物品有数量限制，并且每个不同。
也就是在也来的基础上多了一个数组
C表示价值 W 表示质量， N 表示该物品的有几个可以使用

看了 刚刚，那啥多重背包最暴力的写法的同学可能会直接这样干。

for(int i=1;i<=n;i++){for(int j=m;j>=1;j--){for(int k=0;k<=Math.min(j/w[i],N[i]);k++)
			dp[j]=max(dp[j],dp[j-k*w[i]]+k*C[i])}}

因为我就是这样搞的。怎么优化，还能怎么搞，想办法把第三个循环干掉，或者缩短呗。
干掉，应该是干不掉了，因为有很多问题，会扯到局部与整体的问题。

所以就是相办法先优化这个降低维度。

例如 N[i] = 1000
的时候，我会从 0 到 1000 去试，有没有最好的（假设没有超出范围）那么这里面加入1000次循环。
那这个怎么优化，复杂一点，拆！这里还是大致说一下思路，时间原因。
例如一个物品 i N[i]=4
表示物品i 有四个，那么原来搞的时候，我要遍历4次，目的是拿到 0 1 2 3 4 ,这个时候，我们可以想到蓝桥杯2021年第七题，发现啥了不 4 可以只用几个数字表示例如 1 3 这个玩意可以表示 1 到 4 的所以数字，拿就是加，不拿就是 减。
那么有意思的来了我把这个物品i 拆了 拆成 N[i+1] = 1 N[i+2]=3 假设 对于的N的位置上没有别的物品（也就是假设原来N[i+1],N[i+2] 都为0）此时对应的那个C，W 也添加不就行了。
这里和简单一点的是，直接使用二进制表示就可以了，不用压缩到极致。

这里刚好有一个PTA的题目，来一下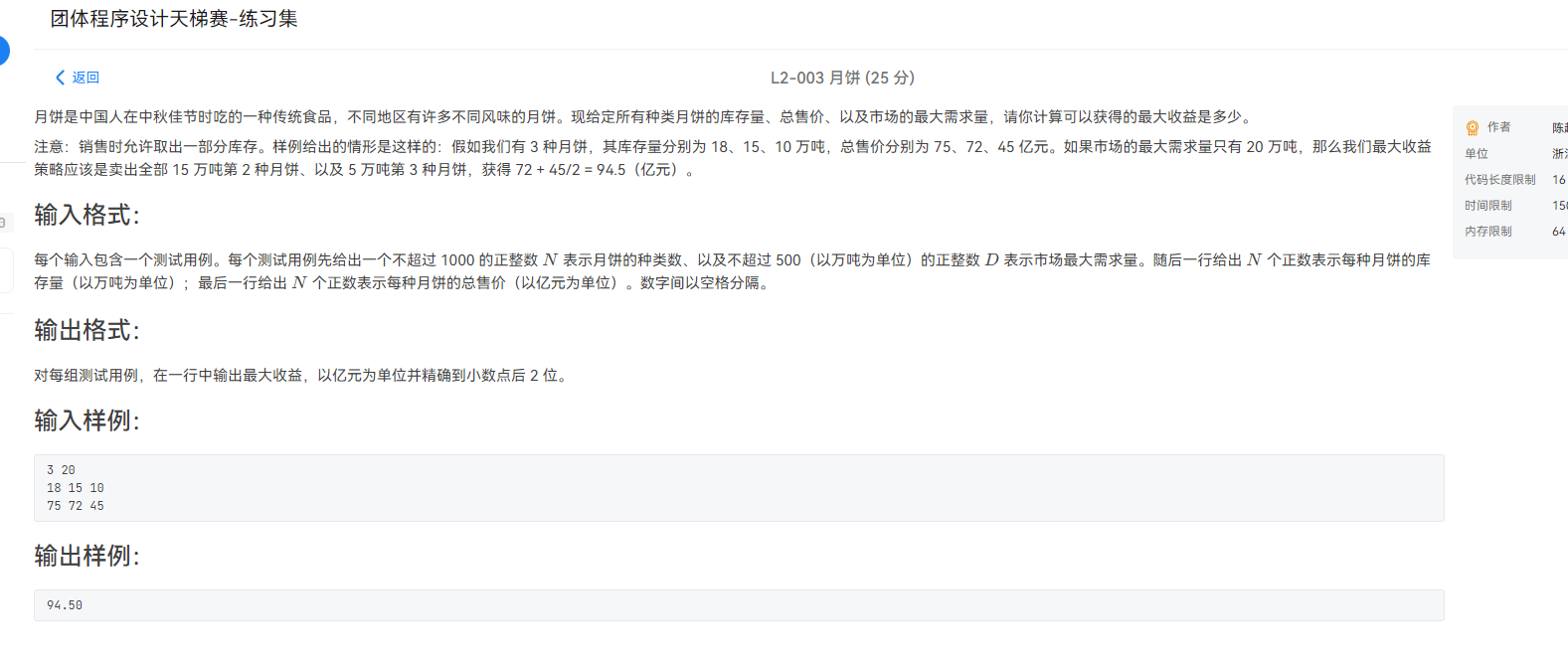

我是直接使用python写的哈。

a,b=(int(i)for iininput().split(" "))

N=[int(i)for iininput().split(" ")]
C=[int(i)for iininput().split(" ")]
dp=[0for _inrange(b+1)]#这里的话它们的质量都是1W吨for iinrange(len(N)):
    C[i]= C[i]/N[i]for iinrange(a):for jinrange(b,0,-1):
        need=min(N[i],j)for kinrange(need+1):
            dp[j]=max(dp[j],dp[j-k]+k*C[i])print("%.2f"%(dp[b]))

这个代码是绝对运行超时了的，也就混个13分

不过这里更好的方式是贪心。但是这里就不提了。

总结

今天就先这样，主要还是思路上的解释，总结。