PyTorch学习-逻辑斯蒂回归

Logistic regression

线性回归输出的是实数，分类问题没有大小之分，输出的是属于某一类的概率

将输出的实数映射到0~1的区间，饱和函数
$sigmoid$ 函数：$\sigma (x)=\frac{1}{1+e^{-x}}$
函数图像：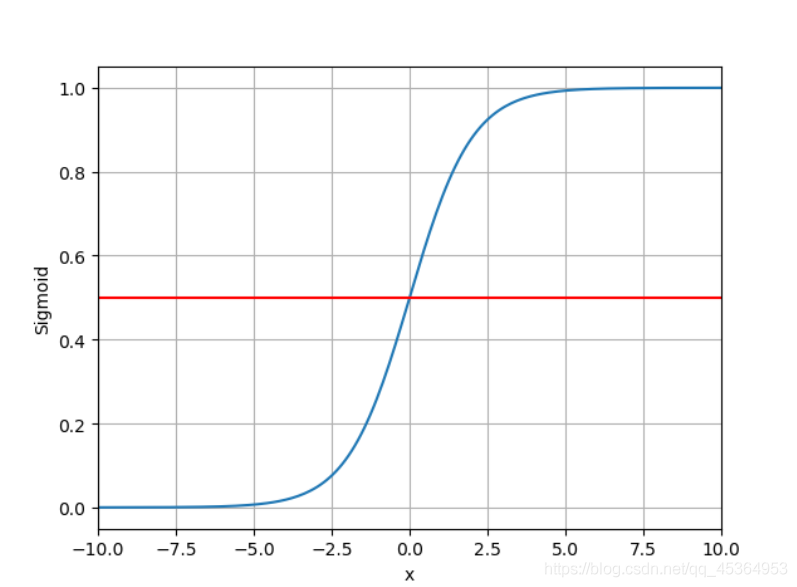

Sigmoid Function有很多，例如 tanh(x)… …

对于二分类的损失函数：y的取值为0、1表示两个类别
BCE loss：$loss=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$
(可求均值或者不求）

交叉熵(cross-entropy)
对于两个分布 $P_D,P_T$
交叉熵：$\sum P_{D_i}\cdot ln(P_{T_i})$

和线性回归模型的区别：
和线性模型相比，构造函数并没有什么区别，但是在forward函数中多了一个sigmoid函数对原来的实数输出进行映射。

数据的准备上，y的值变为0和1

import torch
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)
        
    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred

import torch.nn.functional as F

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)
        
    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x))
        return y_pred

criterion = torch.nn.BCELoss(size_average=False)

model = LogisticRegressionModel()

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()