通过Julia处理高斯光束的光斑图像

基础操作

在Julia中，需要调用Images和ImageView这两个包来实现对图像的读取和处理等操作。在Julia中，下载并安装包的方式为摁下]，使得命令行进入pkg模式，进而使用add命令进行包的获取和安装。包的调用则使用using。安装之后，摁下Backspace删除键，退回命令行模式。

julia>]
(v1.2) pkg>add Images
(v1.2) pkg>add ImageView
julia>using Images, ImageView

在julia中打开图片的命令为load，typeof可以返回数据类型，Gray.可以将RGB图片转为灰度。

julia > img =load("1.bmp");
julia> typeof(img)
	Array{RGB{Normed{UInt8,8}},2}
julia> gray = Gray.(img);
julia> imshow(gray)

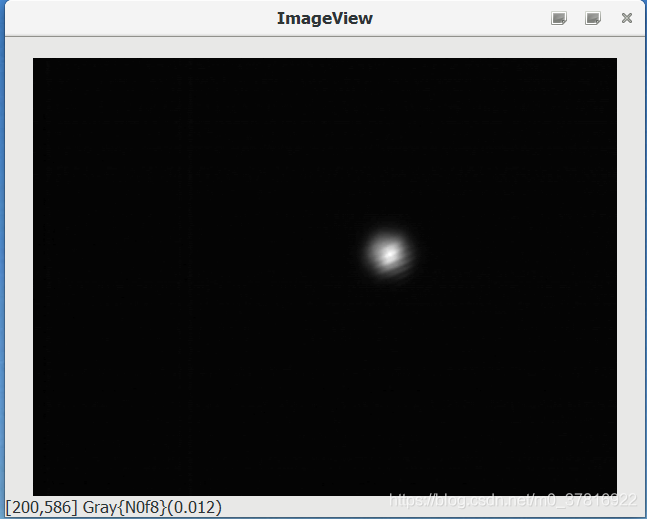
上图中有大量的冗余数据，所以需要对图片进行截取。
当鼠标在图像窗口浮动时，其左下角会显示当前位置的坐标，通过在光斑周边寻找适当的点，得到光斑的大致位置，从而对图片进行截取。
在Julia中，通过方括号进行矩阵索引。

julia> roi = gray[180:244,360:420]		#矩阵截取
julia> imshow(roi)

截取之后的图像为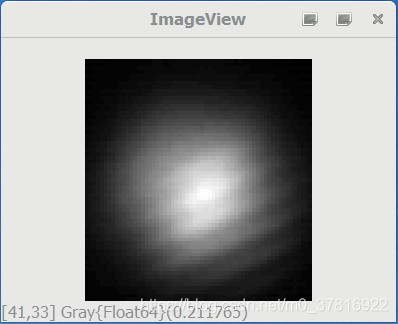

显示强度

通过查看灰度图能够感性地认识到高斯光斑的分布特性，但并不能得到强度之间的对比信息。为了查看强度值信息，首先需要将灰度矩阵转为浮点型矩阵，转换函数为convert。

julia> typeof(roi)
	Array{Gray{Normed{UInt8,8}},2}
julia> roi = convert(Array{Float64,},roi);	#将数据转为浮点型二维数组
julia> typeof(roi)
Array{Float64,2}

在Julia中，画图需要调用Plots包，其绘图命令为plot(x,y,z,seriestype,**kw)，其中，x,y,z分别是三个轴方向的数据，seriestype为图的类型。此外还有一些其他参数，详情可参考官方文档。

julia> size(roi)
(65, 61)
julia> plot(1:61,1:65,roi)
julia> png("JL3.png")			#将图片保存为JL3.png

其默认输出格式为等高线图。

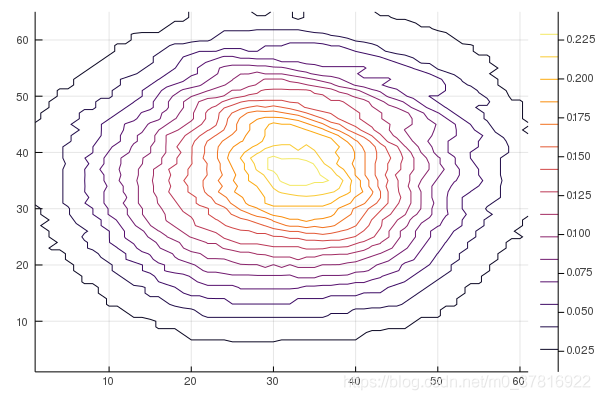
通过将seriestype更改为surface，可以得到其3D曲面图，通过camera参数可以调整视角。

julia> plot(1:61,1:65,roi,seriestype=:surface,camera=(40,40))
julia> png("JL4")

下图即为我们要的3D曲面图。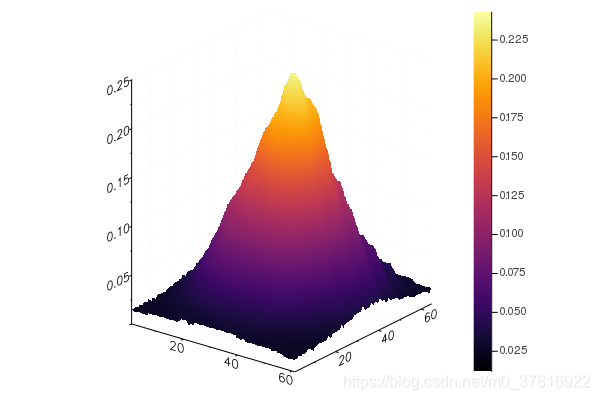

数值拟合

我们现在已经获取了光斑的矩阵数据，现在需要对其进行高斯拟合，由于二维的数据较多，所以我们需要对光斑数据进行择取，在此选取每一列的最大值作为待拟合数据。

julia> arr = [maximum(roi[:,i]) for i in 1:size(roi)[2]]
julia> plot(1:length(arr),arr)
julia> png("JL5")

其中，方括号表示这是一个数组；maximum表示选取最大值，roi[:,i]表示roi的第i列，for循环表示i从1循环到roi的列数。即对每一列选取最大值然后压入数组中。
然后plot画图，png保存。

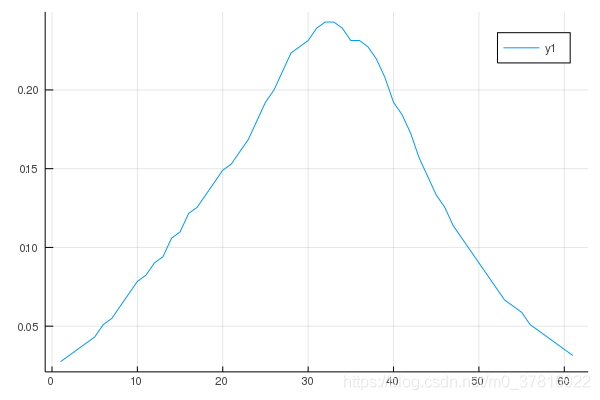
在此，我们通过LsqFit包进行数据拟合，LsqFit是一个基于最小二乘法的数据拟合包，支持线性与非线性拟合。其拟合函数为curve_fit(model,x,y,p0)，其中model为拟合模型，x,y分别为自变量，因变量，p0为参数的初始值。具体说明可参考官方文档。
我们所需要的拟合模型即为光斑的横向分布函数：

$$y=p_1\cdot \exp -(\frac{x-p_2}{p_3}{)}^2$$

其中，$p_1$为光斑强度的最大值，即arr的最大值，$p_2$为光斑最大值所在位置，根据上图知大致在数据中间，$p_3$为当光强降到最大值一半时，其所对应的半径，根据上图知大致为数据长度的四分之一。

julia> using LsqFit
julia> x = 1:length(arr)	#拟合中用到的x值
1:61
julia> p0 = [maximum(arr),length(arr)/2,length(arr)/4]#拟合数据的初始值
3-element Array{Float64,1}:
  0.24313725490196078
 30.5
 15.25
julia> @. model(x,p) = p[1]*exp(-((p[2]-x)/p[3])^2)#gauss模型
julia> fit = curve_fit(model,x,arr,p0);				#拟合表达式
julia> coef(fit)									#返回拟合参数
3-element Array{Float64,1}:
  0.22917383551671539
 31.764775623849907
 19.573161950729897

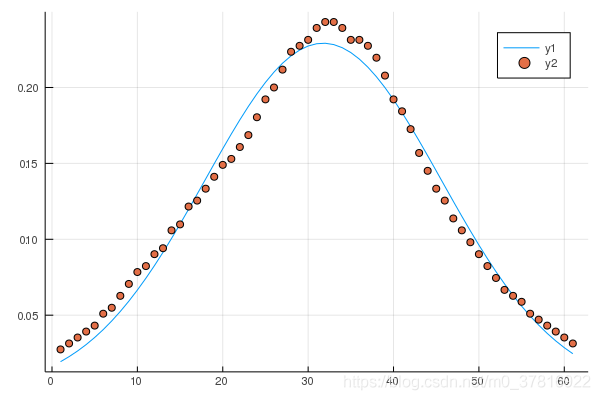
最后，将拟合结果与原数据绘制在一张图中，

julia> y = model(x,coef(fit));	#根据自变量与模型生成拟合后的y
julia> plot(x,[y,arr],st=[:line :scatter])	#seriestype也可写成st
julia> savefit("JL6.png")

效果如图所示