文章目录
第一篇,主要涉及到一些电子通信类专业课的基本定理,和信号处理的基本应用。
001——什么是奈奎斯特采样定理?
奈奎斯特定律即时域采样定理:信号的采样频率要≥信号最高频率的2倍才能满足频域不混叠的条件,才能保证恢复信号时不产生失真。
因为时域采样,会导致频域产生以采样频率为周期的周期性延拓,若周期延拓时,采样频率的1/2低于信号最高频率时,就会导致产生频域混叠现象。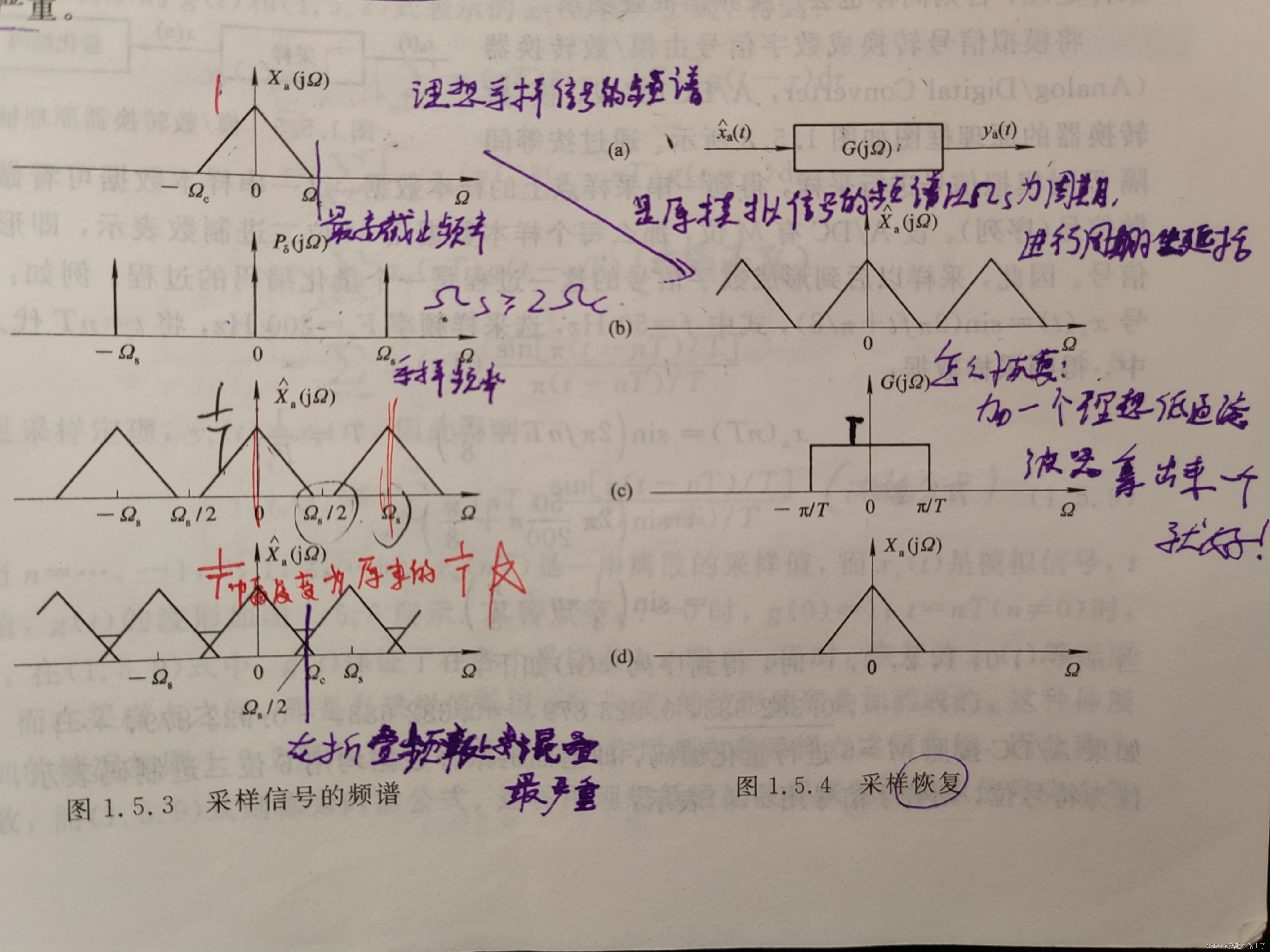
002——有源滤波器和无源滤波器的区别是什么?
有源滤波器需要电源,无源滤波器不需要电源;
有源滤波器可以有增益,无源滤波器无增益,主要看衰减。
003——什么是反馈电路?请举出相关应用
在信号处理中,我理解的反馈电路即:
电路中存在,从信号输出端经过某种反馈反作用给输入端的支路,典型的如IIR滤波器,自适应滤波器等;
反馈电路的概念最初是在大一学的模拟电路课程中了解过,当时主要学的是书本知识和定义,即反馈电路是将放大器输出信号(电压或电流)的一部分或者全部,回送到放大器输入端与输入信号进行比较,并经过比较器得到有效输入信号去控制输出。
在后期的专业课学习和仿真实践中,才更深入地理解了反馈电路的实际工程意义。
004——什么是竞争冒险现象?如何消除和避免此类现象
数字电路中的竞争与冒险出现在组合逻辑电路中。
组合逻辑电路中,同一信号经不同的路径传输后,到达电路中某一会合点的时间有先有后,这种现象称为逻辑竞争,而因此产生输出干扰脉冲的现象称为冒险。
消除方法:
1.选通法:
在电路中加入选通信号,在输出信号稳定后,选通允许输出,从而产生正确输出。
2.滤出法:
由于冒险脉冲是一个非常窄的脉冲,可以在输出端接一个几百微法的电容将其滤出掉。
005——什么是基尔霍夫定理?
基尔霍夫定理是大一电路课程中接触到的第一大定理,包括基尔霍夫电流、电压定理,即:
在任何一个闭合回路中,从任一节点出发绕回路一周回到该节点时,各段电压的代数和恒等于零,即各元件上的电压降的代数和等于电动势的代数和。
基尔霍夫电流定理参考综合电工·2年李先生的回答:
电路中的任何一个节点,在任一瞬间流入一个节点的电流之和等于流出该节点的电流之和。
006——if else语句和case语句的区别?
参考嵌入式·11年开发者江先生的回答:
C语言中,if else语句是逐个对比,switch
case是跳转表。前者空间占用少,但效率低,只有在条件比较少的情况下效率高。后者效率高,但由于有跳转表,所以占空间大一些,只有在条件多的情况下优势比较明显。
if else遇到第一个满足条件的条件就停止往下对比,case是直到遇到第一个break才停止,就去说if
else其实对条件是有优先级的,case没有。
在verilog中,跟c语言相似。
if else占用电路面积小,构建速度快,但是也有条件的优先级,且速度相对慢。case语句正好相反。所以,如果对速度有要求,那么选用case,如果对电路面积有要求就用case。
007——LCD屏和LED屏的区别?
市面上的显示器主要是LED和LCD两大类屏,LCD是指液晶显示屏,而LED是由发光二极管组成的显示器。
从性能上讲,LCD有背光层,通过白光源的折射效果,显示效果更自然,没有屏闪,但不能显示纯黑色,彩度低但不易导致疲劳。LED颜色显示效果更加鲜艳,发光原理和LCD不同,有RGB三色光源,不需要背光层,也不需要液晶层,并且显示屏厚度可以做的很薄且可以弯曲,做成柔性屏,但是LED有屏闪,看久了容易造成实力疲劳。
008——请给出设计IIR滤波器的几种常用方法
直接法和间接法;
间接法借助模拟滤波器来设置数字滤波器,常用的有巴特沃斯型模拟滤波器设计,后经过脉冲响应不变法或双线性变换法将模拟传递函数H(s)设计成数字滤波器H(z);
直接法是利用给出的技术指标, 由数字域幅度平方函数直接进行设计, 它是最方便,也是最易被接受的一种数字滤波器设计方法。
Matlab 双线性变换法设计IIR滤波器方法:
滤除42Hz的信号,保留19Hz的信号
%% IIR数字低通滤波器设计-时域滤波
clc,clear,close all;
%% IIR数字低通滤波器设计-时域滤波
n = -50:50; FS=200; %FS为采样频率
A = 2; F1 = 19; F2 = 42;
origin = A*sin(2*pi*F1/FS*n)+A*cos(2*pi*F2/FS*n); %原始信号
%先确定模拟低通指标
fp=20; fs=30; %fs为阻带截止频率
wp=2*pi*fp/FS; ws=2*pi*fs/FS;
%通带最大衰减和阻带最小衰减
Ap=1; As=50;
wp1=2*FS*tan(wp/2); ws1=2*FS*tan(ws/2);
%确定巴特沃斯模拟低通滤波器阶数
[N1,Wn]=buttord(wp1,ws1,Ap,As,'s');
[z,p,k]=buttap(N1);
[b,a]=zp2tf(z,p,k);
%低通到低通的频率转换,得到模拟域的H(s)分子分母系数
[bt,at]=lp2lp(b,a,Wn);
%确定H(z)数字域的分子分母系数,双线性变换法
[bz,az]=bilinear(bt,at,FS);
figure(1)
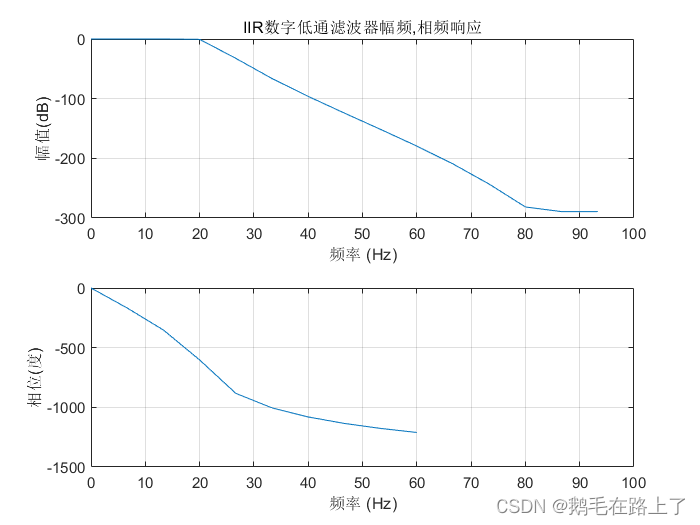
freqz(bz,az,N1,FS); title('IIR数字低通滤波器幅频,相频响应')
outl = filter(bz,az,origin); %IIR滤波器时域滤波
N = length(origin);
out_F1 = abs(fft(outl)/N);
out_F = out_F1(1:N/2+1);
out_F(2:end-1) = 2*out_F(2:end-1);
f = FS*(0:N/2)/N;
figure(2)
subplot(311)
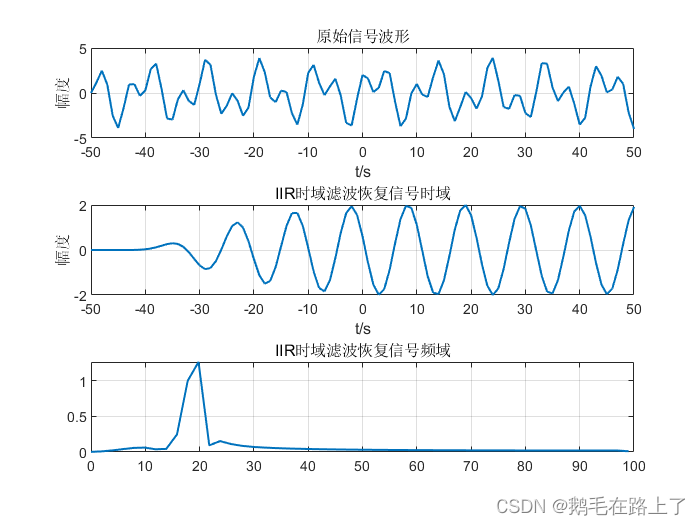
plot(n,origin,'linewidth',1.2)
xlabel('t/s');ylabel('幅度'); title('原始信号波形');
grid on
subplot(312)
plot(n,outl,'linewidth',1.2)
xlabel('t/s');ylabel('幅度'); title('IIR时域滤波恢复信号时域');
grid on
subplot(313)
plot(f,out_F,'LineWidth',1.2); title('IIR时域滤波恢复信号频域');
grid on
009——请给出设计FIR滤波器的几种常用方法
主要有窗函数设计法,和频率采样法设计FIR;窗函数设计法是从时域上去逼近理想带限滤波器的效果,频率采样法是从频域上去逼近,先找出极点,根据传递函数H(s)确定系统函数H(z)。
Matlab 窗函数法设计FIR低通滤波器例程:矩形窗,汉宁窗,海明窗,布拉克曼窗,凯撒窗
计算出结果并绘制幅频特性曲线,也可直接用相关函数绘制出幅频和相频特性。
clc,clear,close all;
fp = 200; fs = 250; FS = 2000; %模拟域指标,单位Hz
%通带截止频率,阻带截止频率,采样频率
%数字频率w = 2*pi*f/Fs
wp = 2*pi*fp/FS; ws = 2*pi*fs/FS; %数字域指标,单位rad
wc = (wp+ws)/2; %3dB截止频率
N = 61; M = 60; %窗长41(阶数60)
b1 = fir1(M,wc/pi,'low',boxcar(N)); %矩形窗设计低通FIR
b2 = fir1(M,wc/pi,'low',hanning(N)); %汉宁窗设计低通FIR
b3 = fir1(M,wc/pi,'low',hamming(N)); %海明窗设计低通FIR
b4 = fir1(M,wc/pi,'low',blackman(N)); %布拉克曼窗设计低通FIR
b5 = fir1(M,wc/pi,'low',kaiser(N)); %凯撒窗设计低通FIR
[h1,w1] = freqz(b1,1,-2*pi:pi/100:2*pi); %freqz求解窗函数法设计FIR的幅频响应
[h2,w2] = freqz(b2,1,-2*pi:pi/100:2*pi);
[h3,w3] = freqz(b3,1,-2*pi:pi/100:2*pi);
[h4,w4] = freqz(b4,1,-2*pi:pi/100:2*pi);
[h5,w5] = freqz(b5,1,-2*pi:pi/100:2*pi);
subplot(511)
plot(w1/pi,20*log10(abs(h1)),'LineWidth',1.2) %20log10(h)转化为dB
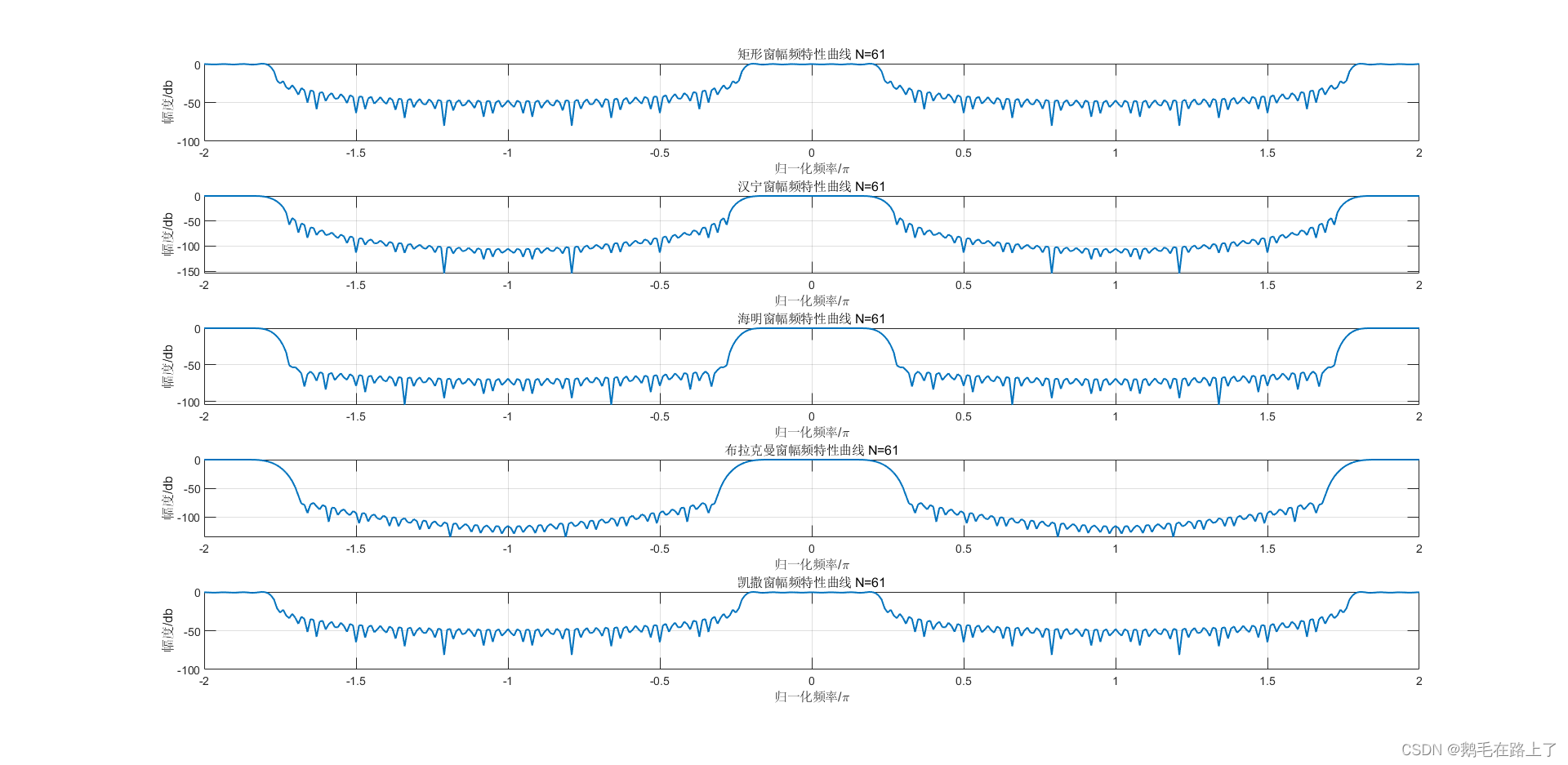
xlabel('归一化频率/\pi'); ylabel('幅度/db');
title('矩形窗幅频特性曲线 N=61')
grid on
subplot(512)
plot(w2/pi,20*log10(abs(h2)),'LineWidth',1.2)
xlabel('归一化频率/\pi'); ylabel('幅度/db');
title('汉宁窗幅频特性曲线 N=61')
grid on
subplot(513)
plot(w3/pi,20*log10(abs(h3)),'LineWidth',1.2);
xlabel('归一化频率/\pi'); ylabel('幅度/db');
title('海明窗幅频特性曲线 N=61')
grid on
subplot(514)
plot(w4/pi,20*log10(abs(h4)),'LineWidth',1.2);
xlabel('归一化频率/\pi'); ylabel('幅度/db');
title('布拉克曼窗幅频特性曲线 N=61')
grid on
subplot(515)
plot(w4/pi,20*log10(abs(h5)),'LineWidth',1.2);
xlabel('归一化频率/\pi'); ylabel('幅度/db');
title('凯撒窗幅频特性曲线 N=61')
grid on
010——请说明阶数对于矩形窗、广义余弦窗的影响,不同窗函数有什么特点和指标?
汉宁窗以使用旁瓣互相抵消,消去高频干扰和漏能,从减小泄漏观点出发,汉宁窗优于矩形窗。但汉宁窗主瓣加宽,相当于分析带宽加宽,频率分辨力下降;
海明窗和汉宁窗函数的主瓣宽度是一样大,只是加权系数不同。海明窗加权的系数能使旁瓣达到更小;
这个窗函数和前两个窗函数很像,不过增加了升余弦的二次谐波分量,旁瓣峰值衰减增大。