一、汉诺塔问题

古人往往很有智慧，解决传说中的难题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？（每次只能移动1个盘子，大盘子只能放在小盘子下面）

二、汉诺塔问题图解

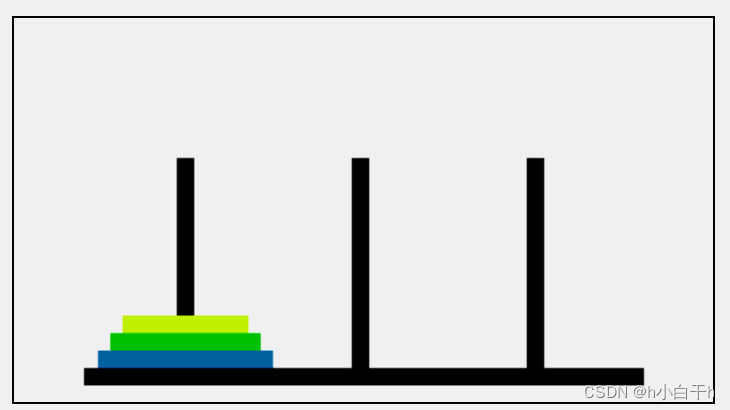
三、汉诺塔问题详解

首先我们可以通过盘子移动的规律来总结得到递推公式：
1个圆盘的时候 2的1次方减1
2个圆盘的时候 2的2次方减1
3个圆盘的时候 2的3次方减1
4个圆盘的时候 2的4次方减1
5个圆盘的时候 2的5次方减1
…

*f(n)=f(n-1)2+1;

通过盘数奇偶 根据步骤 具体实现
塔数 步骤
1 A->C
2 A->B、A->C、B->C
3 A->C、A->B、C->B、A->C、B->A、B->C、A->C
4 A->B，A->C，B->C，A->B，C->A，C->B，A->B，A->C，B->C，B->A，C->A，B->C，A->B，A->C，B->C
… …
偶 A->B
奇 A->C

可以总结出
当n是偶数时
1）奇数步骤一定有a->b,b->c,c->a,a->b的重复顺序输出
2）偶数步骤一定有固定的7对序对输出顺序，为
a->c,a->b,c->b,a->c,b->a,b->c,a->c
当n是奇数时
1）奇数步骤一定有a->c,c->b,b->a,a->c的重复顺序输出
2）步骤为2，2+4，2+4+4…一定有a->b,b->c,c->a,a->b的重复顺序输出
3）步骤为4的倍数时一定有7个对固定输出顺序，为
a->c,a->b,c->b,a->c,b->a,b->c,a->c

**

四、汉诺塔代码实现

import java.util.Scanner;

public class Hanoi {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入汉诺塔盘数:>");
        int n = scanner.nextInt();
        hanoi(n, 'A', 'B', 'C');
    }

    public static void hanoi(int nDisks, char A, char B, char C) {
        if (1 == nDisks) {
            move(nDisks, A, C);
            return;
        }
            hanoi(nDisks - 1, A, C, B);
            move(nDisks, A, C);
            hanoi(nDisks - 1, B, A, C);
        }


    private static void move(int nDisks, char sourceTower, char destTower) {
        System.out.println("编号为" + nDisks + "的盘子正在从" + sourceTower + "移动到" + destTower);
    }
}

**
测试图示(几次调试，终于成功nice！)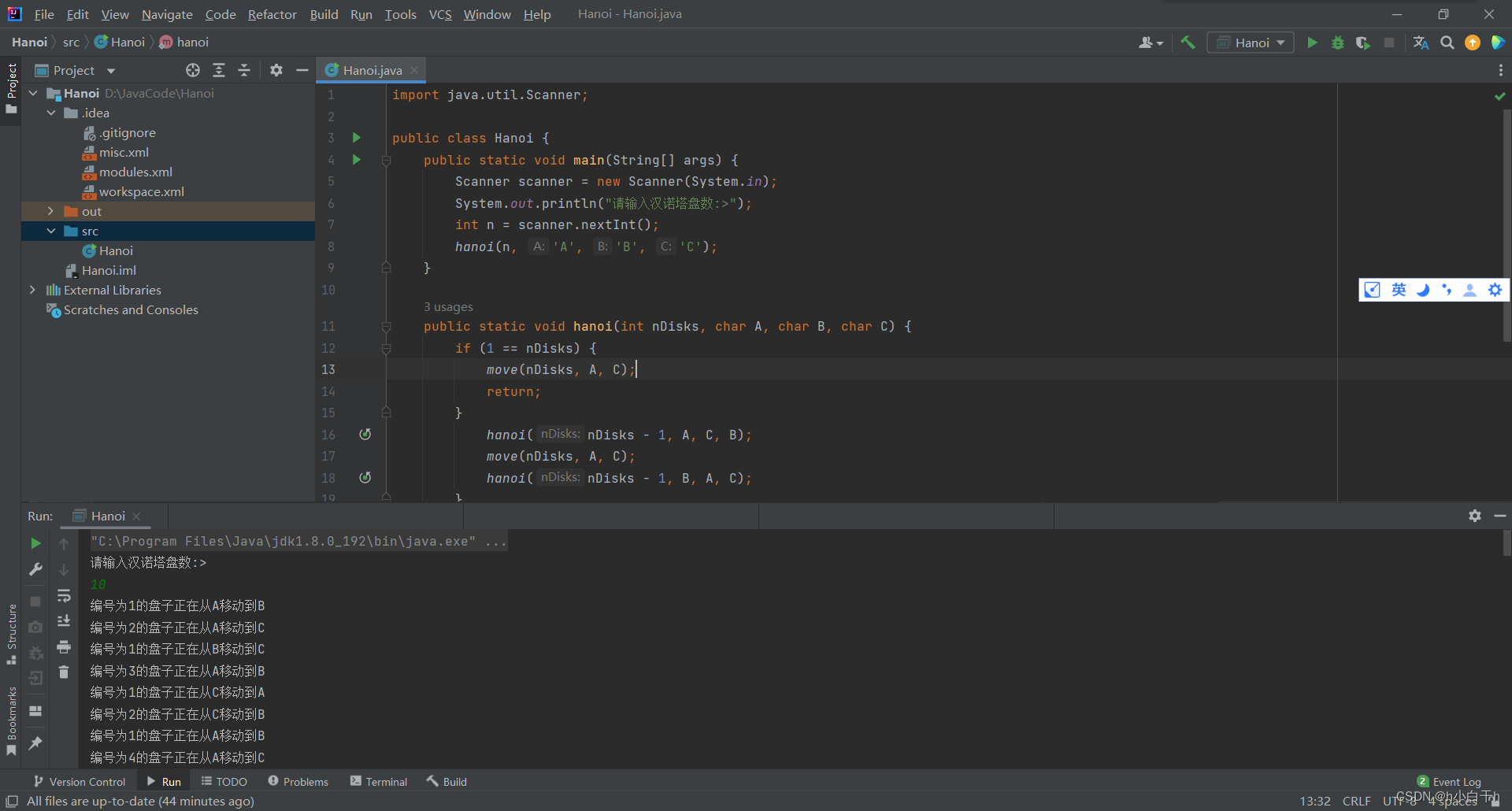

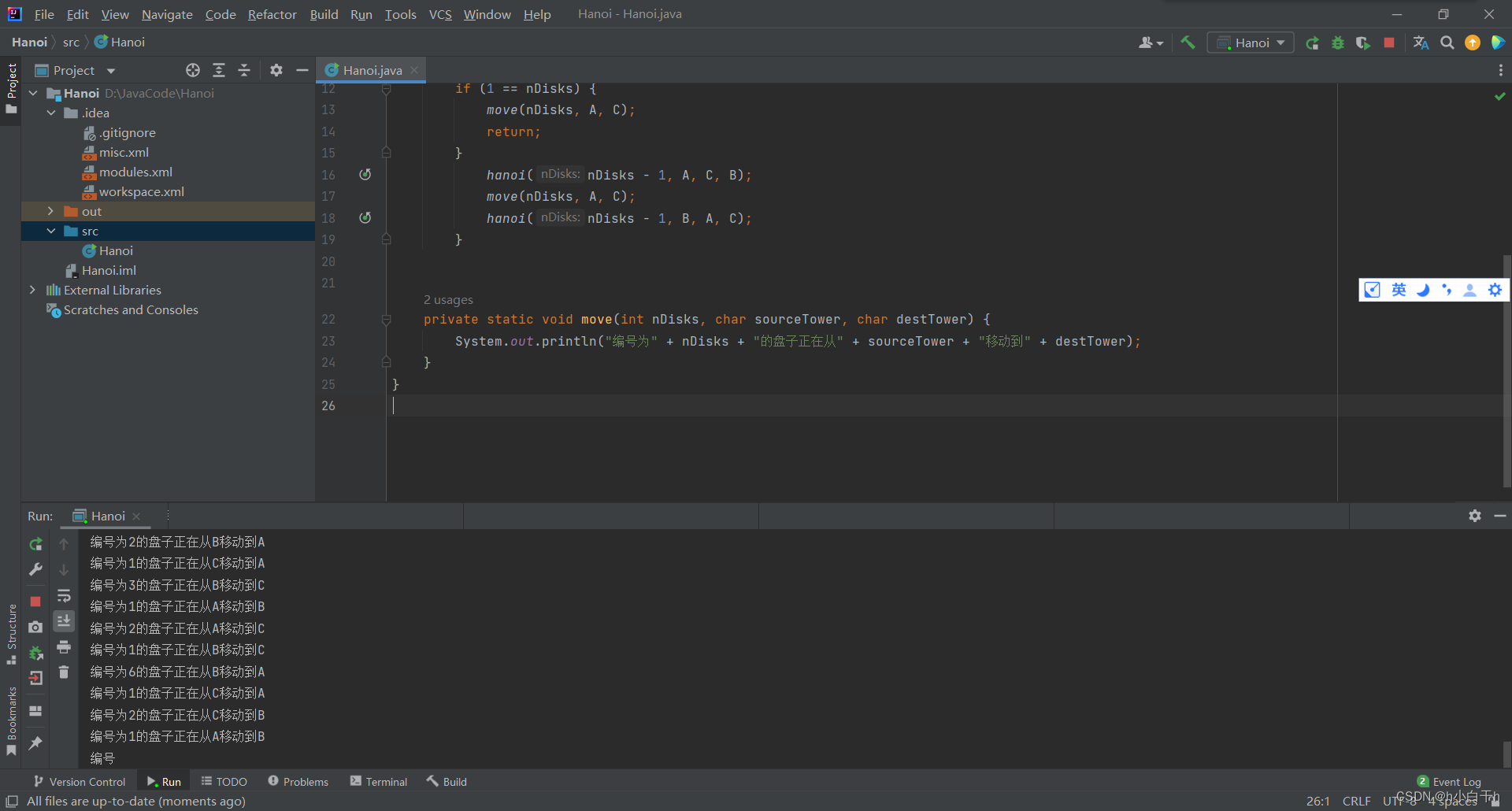
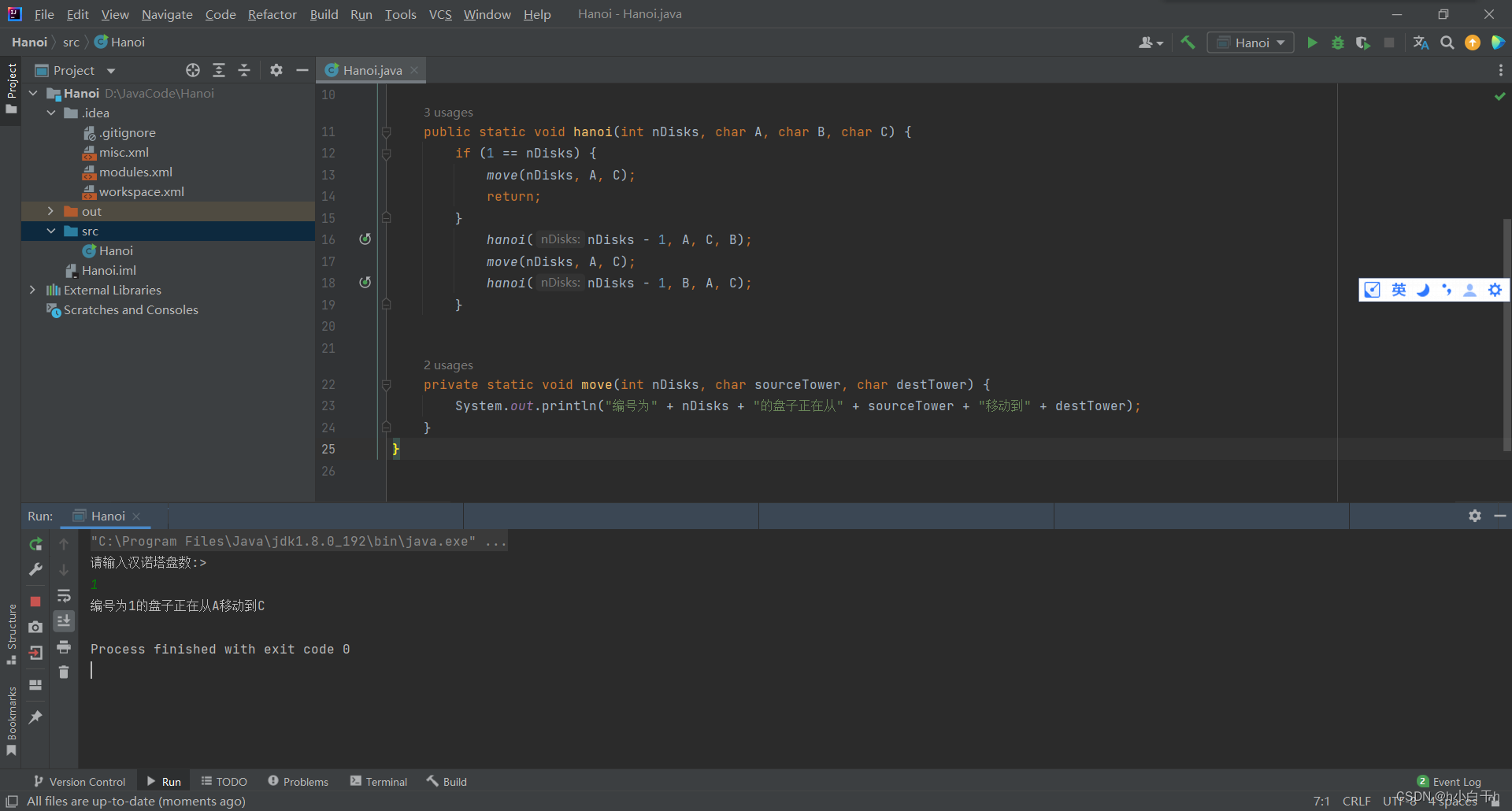
最后说一下写代码中间遇到的问题：

int类型传参参数名不能和函数里定义名一样，这个是很好注意的。
如：调用函数里是n，传参时是写的是nDisks。
其他类型如char类型不一定。
因为char类型在函数里被定义本身是保存在内存里的ASCII值。
调用时对应的是其字符，所以编译器没有报错。

在java中调用方法可以没有返回值，用void参数类型来表示，但是用return可以提前结束被调函数。

最后感谢您的观看，觉得写的不错不妨点个赞，关注就没不好意思要了，本身基础薄弱写的很少也不更新就不占用你的关注位了。如果那里有错误，欢迎指出，一起讨论，初学者很需要被纠错。