纠错编码的基本原理
3位二进制数字构成的码组,共有8种不同的组合。任一码组在传输中若发生一个或多个错码,将变成另一信息码组,此时无法发现错误。若如下所示,使用部分码字,则接收端在某一位发生错误时,可以发现一个错码。但是这种码不能发现两个错码,因为发生两个错码后产生的是许用码字。该码只能检测错误,不能纠正错误,当收到的码组为禁用码字100时,无法判断时哪一位码发生了错误,如000、101、110都可能变成100。要想能纠正错误,还要增加冗余度。
000
001(不可用)
010(不可用)
011
100(不可用)
101
110
分组码和线性分组码
信息码分组,每组信码附加若干监督码,称为分组码。(n, k)表示分组码,n为码组长度(码长),k为信息码长,m=n-k为监督码长。
码重:“1”的数量称为码重。
码距:两个码字对应位置上数字不同的位数称为码字的距离,又称汉明距离。
最小码距:某种编码中各个码字间距离的最小值称为最小码距d。(即校验矩阵H中任意(d-1)列线性无关)
最小码距与码的纠错能力有以下关系:
(1) 检测e个随机错误,要求d≥e+1;
(2) 纠t个随机错误,要求d≥2t+1;
(3) 纠t个随机错误,同时检测e(e≥t+1)个随机错误,要求d≥e+t+1。
奇偶监督码的编码原理利用了代数关系式,这类建立在代数学基础上的编码称为代数码,在代数码中常见的是线性码。线性码中信息位和监督位是由一些线性代数方程联系起来的,或者说线性码是按一组线性方程构成的。
汉明码
汉明码(Hamming Code)是由Richard Hamming于1950年提出的,属于线性分组码的范畴,其基本原理是将信息码元与监督码元通过线性方程式联系起来的,每一个监督位被编在传输码字的特定比特位置上。系统对于错误的数位,无论是原有信息位中的,还是附加监督位中的都能把它分离出来。各种码之间的大致关系如下: 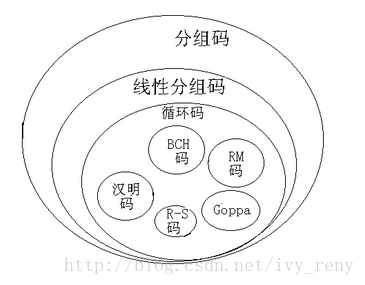
标准汉明码的码长n=2^m-1,监督位数为m,信息位数为k=n-m,最小码距d=3,因此它的纠错能力t=1,是一种常用纠单个位错误的编码方式。还可以根据需要对标准汉明码进行扩展,增加1个校验位对所有位进行监测,就得到扩展汉明码。1个(n,k)汉明码经过扩展以后,就变成了(n+1,k)汉明码。扩展以后的汉明码d=4,t=2,e=1,可以纠正单个位错误,并检测出双位的错误。
Hamming Rule
m个监督位构造出m个监督关系式,指示一种错码的n种可能位置,则
2^m≥n+1=k+m+1
(7,4)汉明码示例
设信息位4位,校正子3位,(7,4)汉明码用a6,a5,…a0表示这7个码元,用S1,S2,S3表示三个监督关系式中的校正子,校正子与错码位置的对应关系如下规定(这个规定是任意的):
| S1 S2 S3 | 错码位置 |
|---|---|
| 001 | a0 |
| 010 | a1 |
| 100 | a2 |
| 011 | a3 |
| 101 | a4 |
| 110 | a5 |
| 111 | a6 |
| 000 | 无错 |
按照表中的规定可知,仅当一个错码位置在a2,a4,a5或a6时校正子S1为1,否则S1为0。这就意味着a2,a4,a5,a6四个码元构成偶校验关系:
S1 = a6⊕a5⊕a4⊕a2
同理,可以得到:
S2 = a6⊕a5⊕a3⊕a1
S3 = a6⊕a4⊕a3⊕a0
在发送信号时,信息位a6,a5,a4,a3的值取决于输入信号,是随机的。监督为a2,a1,a0应该根据信息位的取值按照监督关系决定,即监督位的取值应该使上述(1)(2)(3)式中的S1,S2,S3为0,这表示初始情况下没有错码。即
S1=a6⊕a5⊕a4⊕a2 = 0
S2=a6⊕a5⊕a3⊕a1 = 0
S3=a6⊕a4⊕a3⊕a0 = 0
由上式进行移项运算,得到:
a2 = a6⊕a5⊕a4
a1 = a6⊕a5⊕a3
a0 = a6⊕a4⊕a3
已知信息位后,根据上式即可计算出a2,a1,a0三个监督位的值。
接收端收到每个码组后,先按监督方程计算出S1, S2, S3,再按表格判断错码情况。
线性分组码的一般原理
上述信息位和监督位满足的线性方程可以表示为: 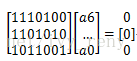
记为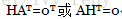
H=[P Ir]称为监督矩阵,H矩阵各行是线性无关的,行数=监督位数,列数=码字长度 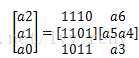
转置得 
G = [Ik Q]称为生成矩阵,生成矩阵G的每一行都是一个码字。 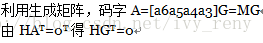
(n,k)线性分组码的生成矩阵G和校验矩阵H分别为k×n和(n-k) ×n维矩阵,其中校验矩阵H决定信息位与校验位的关系,在编码和译码中都要用到。 
译码
若发送码组为A,接收码组为B,二者之差E=B-A,E称为错误图样。 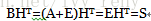
当接收码组无错时,S=0,有错但不超过检错能力时,S不等于0,当错码超过检错能力时,S仍等于0,这样的错码是不可检测的。S称为校正子(伴随式),S只与E有关,而与A无关,S与E有线性变换关系,与E一一对应,可指示错码位置。
伴随式译码,是由接收码B和校验矩阵H算出伴随式S,再根据S就可以算出E,判断哪一位发生了错误并纠正。标准阵列译码法是一种非常直观的方法,标准阵列有2^m行,2^k列,包含了所有2^n种可能的n维二元向量。
校验算法设计
首先根据原始信息码长确定需要多少个监督位。
再确定监督位和信息位的码字位置,确定伴随式(监督位)和错码位置的关系。
根据偶监督测试原理,可知监督位参与了哪几个码位上的计算,得到生成矩阵/生成方程。
接收码后,由校验矩阵计算出伴随式,根据伴随式计算出错误图样,哪一位发生了错误并纠正。
(72, 64)扩展汉明码
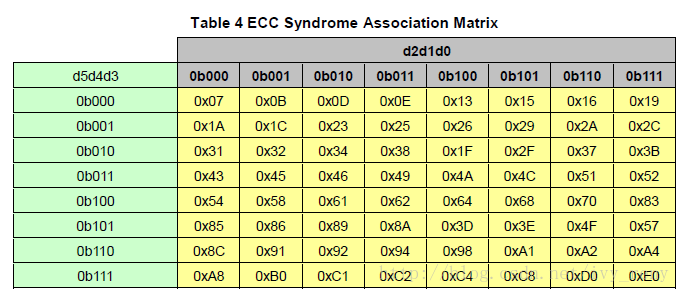
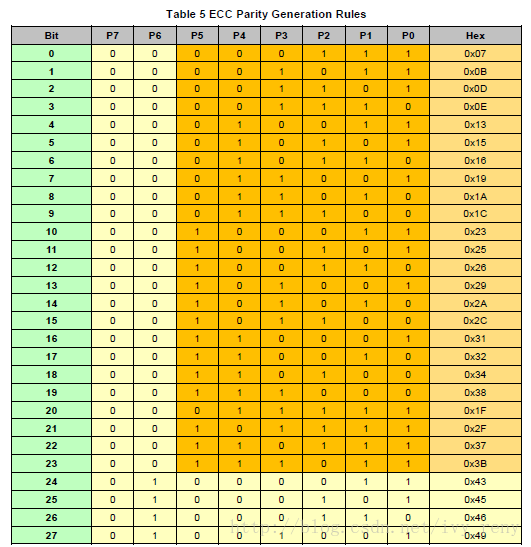
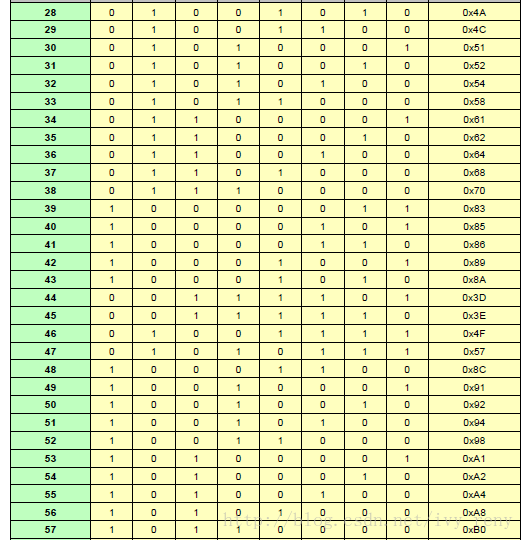
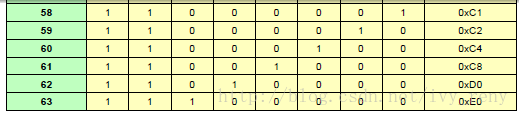
矩阵中的值代表伴随式P7P6P5P4P3P2P1P0,d5d4d3d2d1d0指示0~63位哪一位数据发生了错误。根据发送和接收数据,计算出8 bit ECC(PSEND和PRECV)。伴随式S=PSEND^PRECV。如果没有错误,S=0;出现单比特错误时,S为上表中某一数值;如果S只有1bit为1,则错误位在ECC中;如果S不在上表中,说明出现2位或以上错误。
下表是ECC编码规则: