文章目录

---

前言

众所周知，约瑟夫问题又名丢手绢问题，是一个经典的算法问题。这里就以丢手绢问题来模拟约瑟夫问题的大致内容。问题的大致内容是：已知n个小孩（以编号1，2，3.....，n)围成一个圈。从编号为k的人开始报数，数到m的那个人出列，出列之后，剩下的人又继续报数，同时他的下一个人又从1开始报数，数到m的那个人又出列，剩下的人又继续报数。以此规律重复下去，直到小孩全部出列。

如图，这里以6个小孩作为例子说明问题：这里有6个小孩围成一个圈

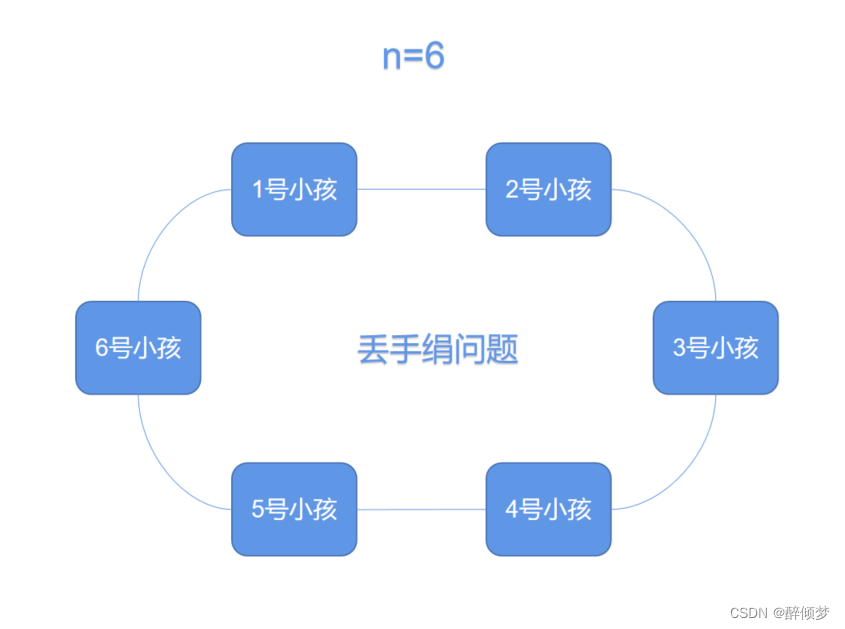
当k=1，m=3时，表示从第一个小孩开始报数，数到第三个小孩时，小孩出列。

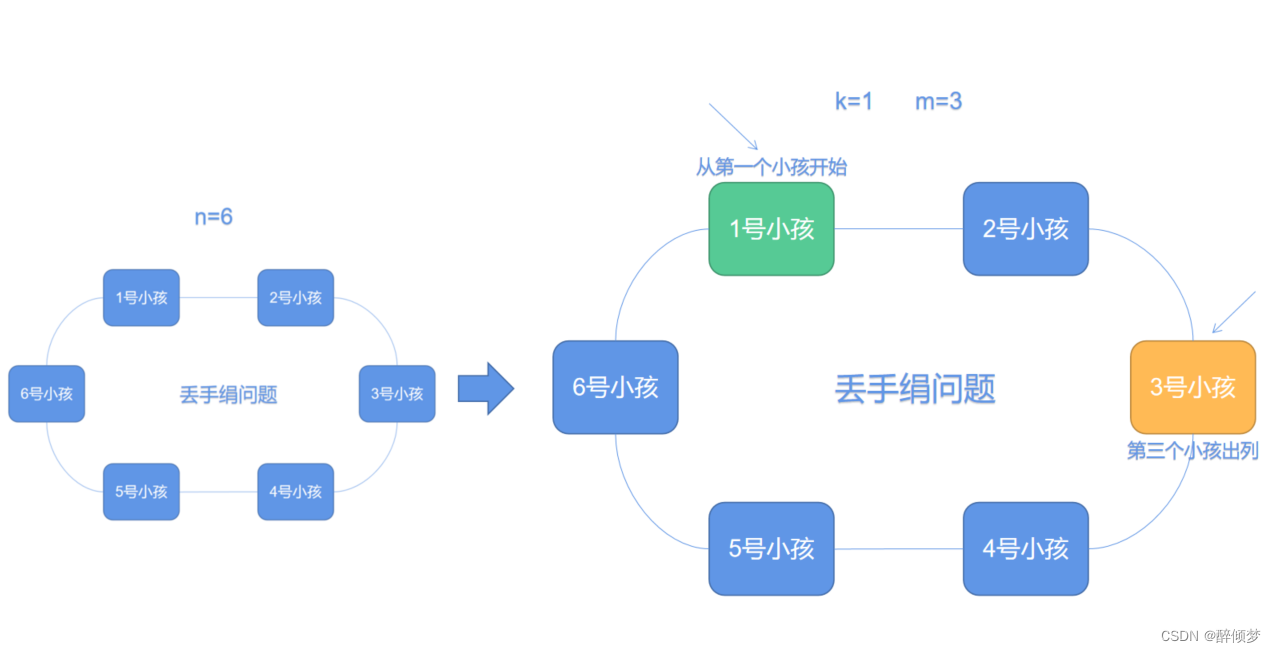
当第三个小孩出列之后，队伍中只剩下5个小孩，同时，此时从4号小孩开始报数，数到3时，第6个孩子出列。

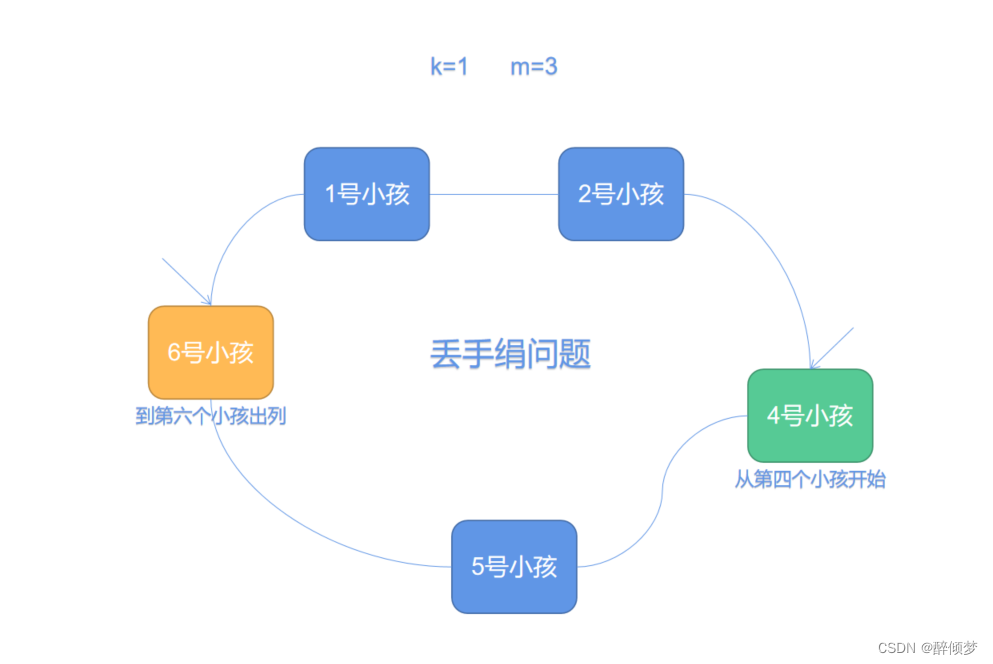
六号孩子出列之后，场上仅剩下1,2,4,5号小孩，他们四个小孩也进行同样的操作。

以此类推，当最后一个小孩出列时，游戏结束。

---

一、思路分析

在本篇文章中，我们将使用Java语言中的链表来解决约瑟夫问题（丢手绢问题）。

由上述所知，该文章一共有n个小孩，从第k个小孩开始报数，报到第m个小孩时小孩出列，剩下的小孩接着报数。在上方的图解中，我们可以清晰的看出，这些小孩围在一起形成了一个环，当数到第n个小孩时，该环又重新轮回到第1个小孩处，继续报数。在这里，我们可以制作一个环形链表来解决这个问题。我们把这个环叫做约瑟夫环，以下是实现的图解：

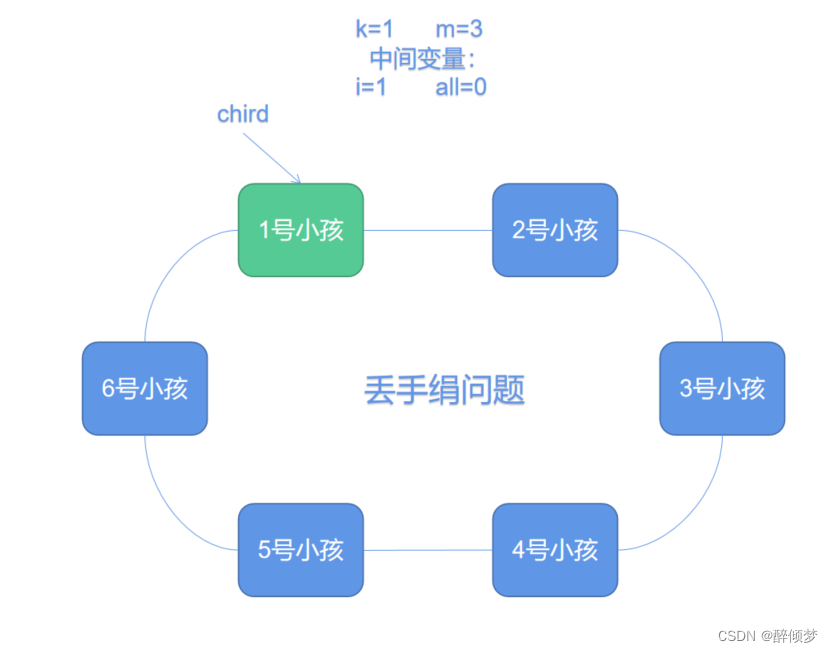
在这里，我们可以利用两个中间变量来进行问题的解决。其中，i变量是从1开始，表示当前报数报的是多少，all则表示当前已经出列了多少个小孩，如果小孩都出列完成，则程序运行结束。

在这里，我们使用chird来代表小孩，当开始数数时，从第k个小孩开始数，这里就是从第1个小孩开始，当1号小孩报数之后，由2号小孩进行报数，此时2号小孩报2，则中间变量i就等于2。

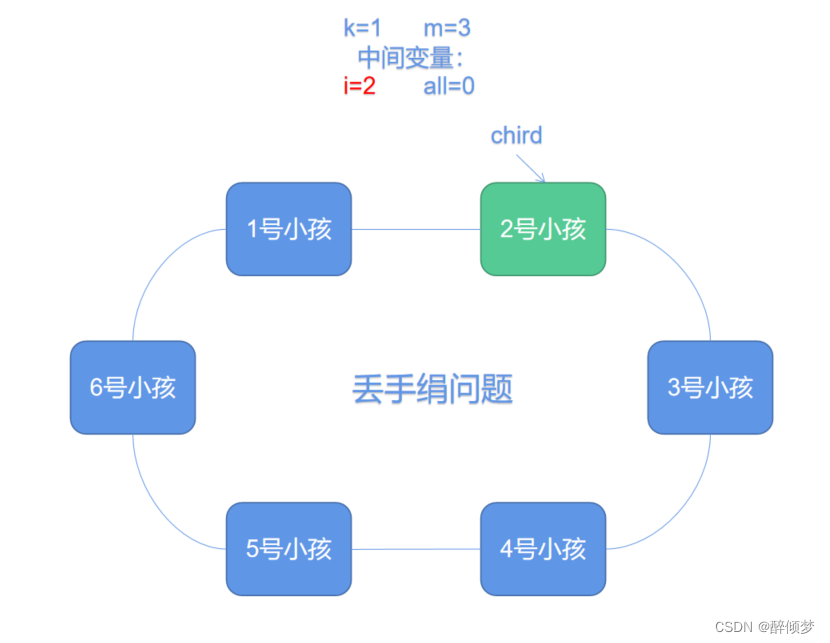
当报到第三个小孩时，3号小孩报3，此时与m相同，则3号小孩出列，当循环到4号小孩时，i又等于1，重新在环中继续报数

 

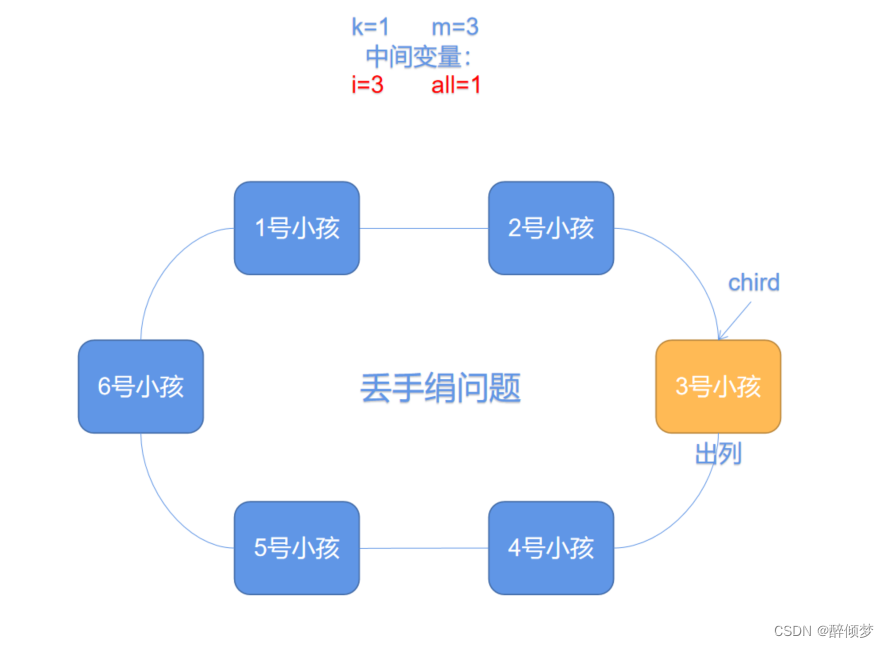
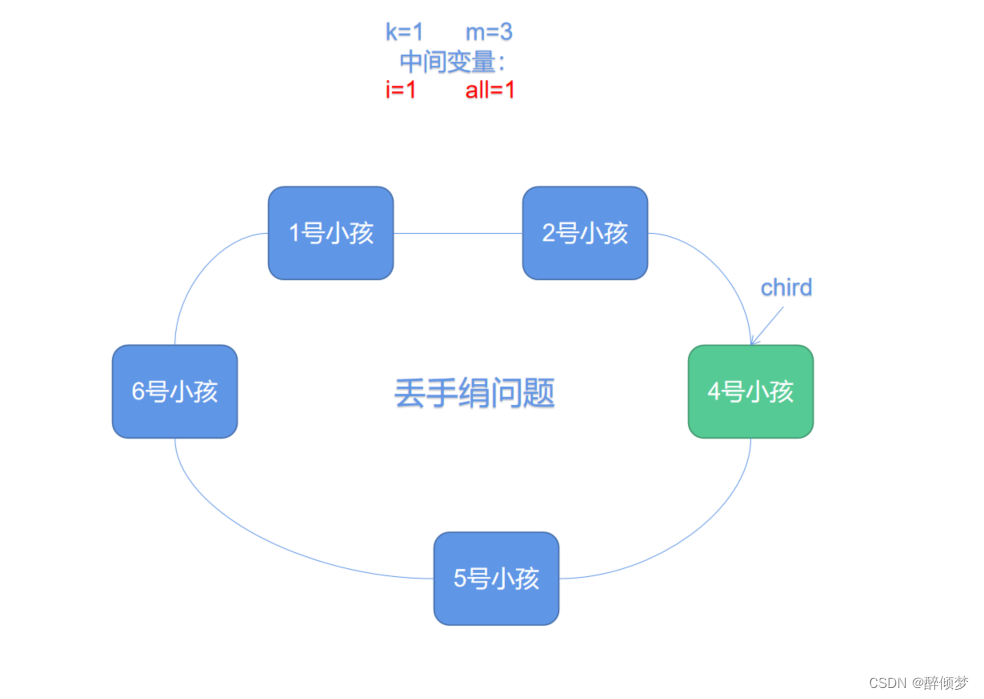
在这个过程中，chird代表当前正在报数的小孩。但是在实际编写环形链表的过程中，会出现一个“头小孩”的问题，我们要将报第一个数的小孩当做头小孩，以这一个小孩为基准，利用i这个中间变量来获取第i个小孩，从而解决问题。当i=m时，第i个小孩出列，此时将出列之后的下一个小孩重新当做“头小孩”，以此来进行环形链表的获取。

二、代码实现

1.Chird类的实现

为模拟小孩，在该类中我们重新创建了一个新类Chird来表示小孩，该小孩拥有id，以及下一个小孩的属性next，拥有一个构造函数来new一个小孩，拥有一个toString方法来对小孩信息进行打印，代码如下：

class Chird {
    int id;
    Chird next;
    public Chird(int id) {
        this.id = id;
    }

    @Override
    public String toString() {
        return "小孩id = "+this.id;
    }
}

2.链表的创建

在该类中，我们创建了一个单向链表新类，名为ChirdLinkedList，在这个类中，我们首先要定义一个“虚拟的头小孩”（头指针），有了这个“虚拟的头小孩”（头指针）之后，我们才可获取到第一个小孩。同时，我们在链表中实现了将单向链表转换为环形链表，已经链表的增删查功能。代码如下：

class ChirdLinkedList {
    Chird head = new Chird(0);
    //将链表更改为环形链表
    public void toCircularLinked() {
        Chird temp = head;
        if (temp.next == null) {
            return;
        }
        while (true) {
            if (temp.next == null) {
                temp.next = head.next;
                break;
            }
            temp = temp.next;
        }
    }
    // 更改头小孩
    public void changeHeadNext(Chird chird) {
        head.next = chird;
    }
    // 获取第i个小孩（相对于头小孩）
    public Chird getChird(int num) {
        if (num < 1) {
            return null;
        }
        int i = 0;
        Chird temp = head.next;
        while (temp != null) {
            i++;
            if (i == num) {
                return temp;
            }
            temp = temp.next;
        }
        return null;
    }
    //新增小孩
    public void addChird(int num) {
        Chird temp = head;
        while (true) {
            if (temp.next == null) {
                for (int i = 1; i <= num; i++) {
                    Chird chird = new Chird(i);
                    temp.next = chird;
                    temp = temp.next;
                }
                break;
            }
            else {
                temp = temp.next;
            }
        }
    }
    //删除小孩
    public void deleteChird(int num) {
        if (num < 1) {
            return;
        }
        int i = 0;
        Chird temp = head;
        while (temp.next != null) {
            i++;
            if (i == num) {
                if (temp.next == head.next) {
                    head.next = temp.next.next;
                }
                temp.next = temp.next.next;
                return;
            }
            temp = temp.next;
        }
        return;
    }
}

3.功能的实现

在实现了小孩和链表之后，我们就可以利用此对功能进行实现了。

public static void main(String[] args) {
        solveJosephQuestion(6,2,3);
    }

    public static void solveJosephQuestion(int n, int k , int m) {
        ChirdLinkedList chirdLinkedList = new ChirdLinkedList();
        chirdLinkedList.addChird(n);
        chirdLinkedList.toCircularLinked();
        Chird chird = chirdLinkedList.getChird(k);
        //更改第k个小孩为头小孩
        chirdLinkedList.changeHeadNext(chird);
        int i = 1;
        int all = 0;
        while (true) {
            if (i == m) {
                //输出出列的小孩名称
                System.out.println(chird.toString());
                all ++;
                //删除小孩并更改头小孩
                Chird chird2 = chirdLinkedList.getChird(m+1);
                chirdLinkedList.deleteChird(m);
                chirdLinkedList.changeHeadNext(chird2);
                //i归零
                i=0;
                //如果小孩总数等于出列小孩总数则退出循环
                if (n==all) {
                    return;
                }
            } else {
                //i累加
                i++;
                chird = chirdLinkedList.getChird(i);
            }

        }
    }

---

总结

以上就是利用环形链表实现约瑟夫问题（丢手绢问题）的过程，在这个过程中主要创建了小孩类和链表类，分别实现了不同的功能，最后在函数中解决了约瑟夫问题（丢手绢问题），在实际编程的过程中还是要非常注意逻辑关系和编写顺序，如果中间的一些关键步骤顺序错了也会导致最后的结果错误喔~