问题抽象:Python如何绘制曲线的阴影图?
===============================
建议的方案:
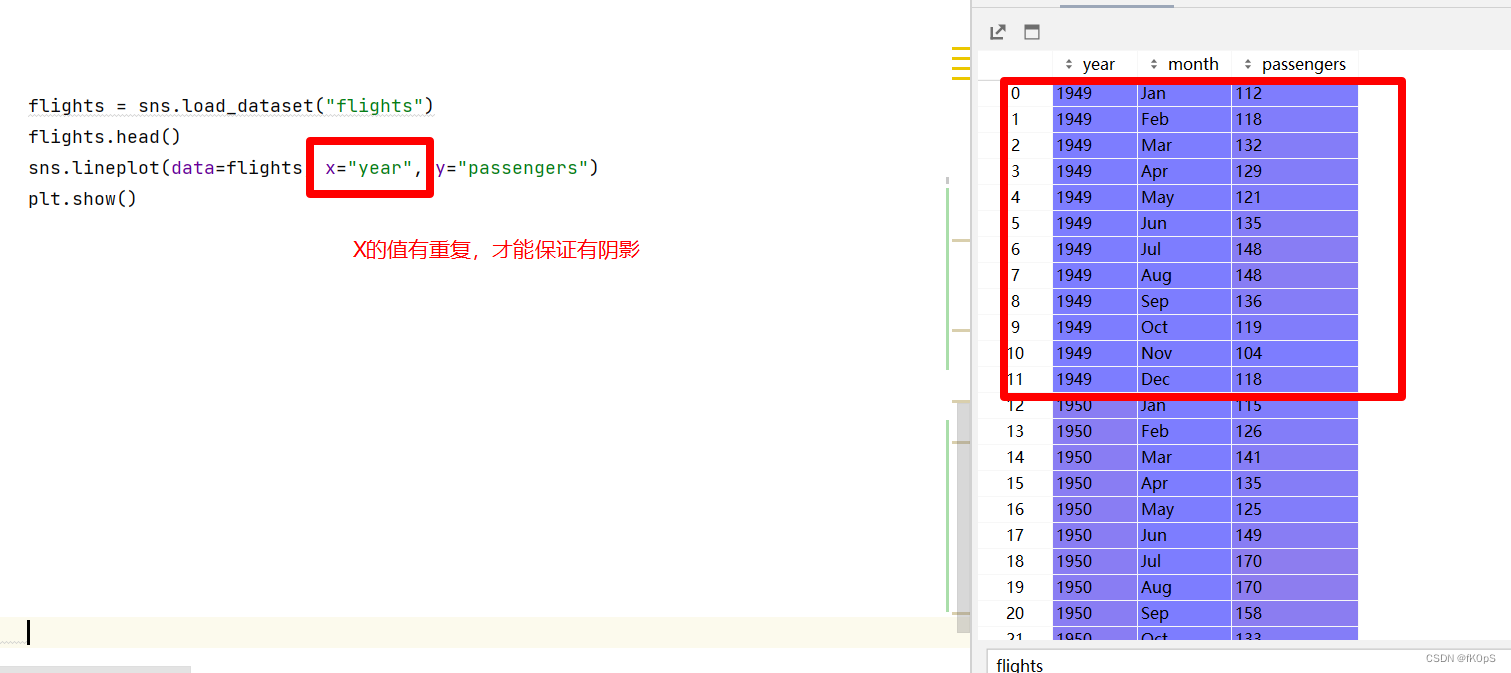
flights = sns.load_dataset("flights")
flights.head()
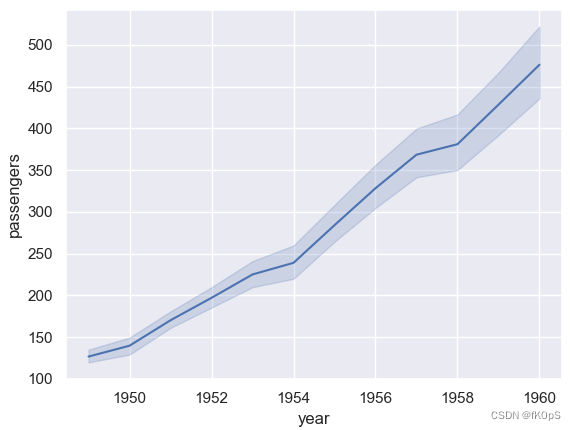
sns.lineplot(data=flights, x="year", y="passengers")
plt.show()
效果如下图:
=============================
方案1:
shade range graph
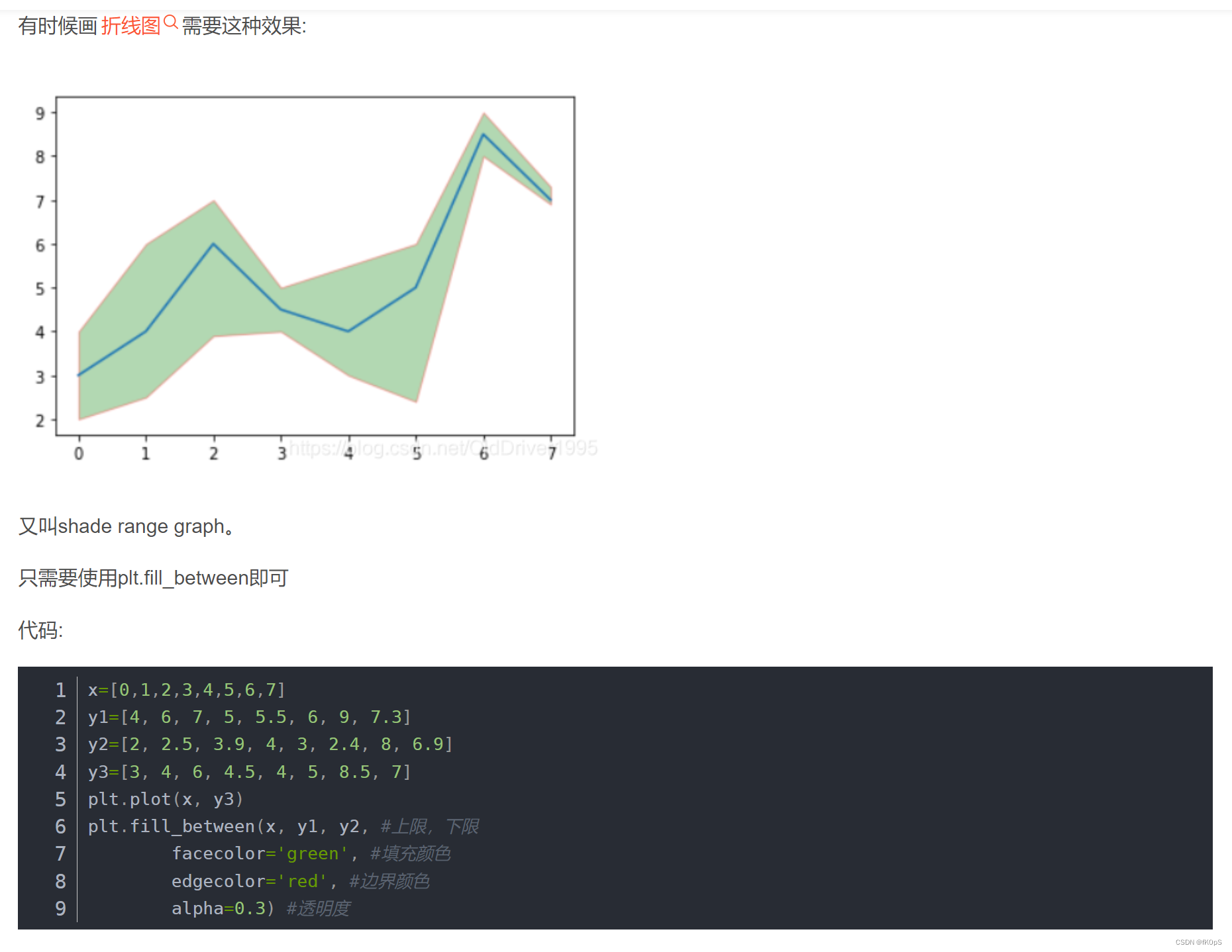
python带阴影范围的折线图_FrenchOldDriver的博客-CSDN博客_matplotlib 折线图区间阴影
这个方法的弊端是,需要构造三条曲线,y1和y2.确定上下边界。难道没有方法,能够根据多条曲线,自动确定这个边界吗?
方案2:
按照下边的方法,实践了一下后,发现没有阴影的效果啊。
lineplot

Seaborn可视化 -- 折线图seaborn.lineplot - 知乎
方案3,这不是我想要的结果:
方案4:
这里有答案,
seaborn.lineplot — seaborn 0.11.2 documentation
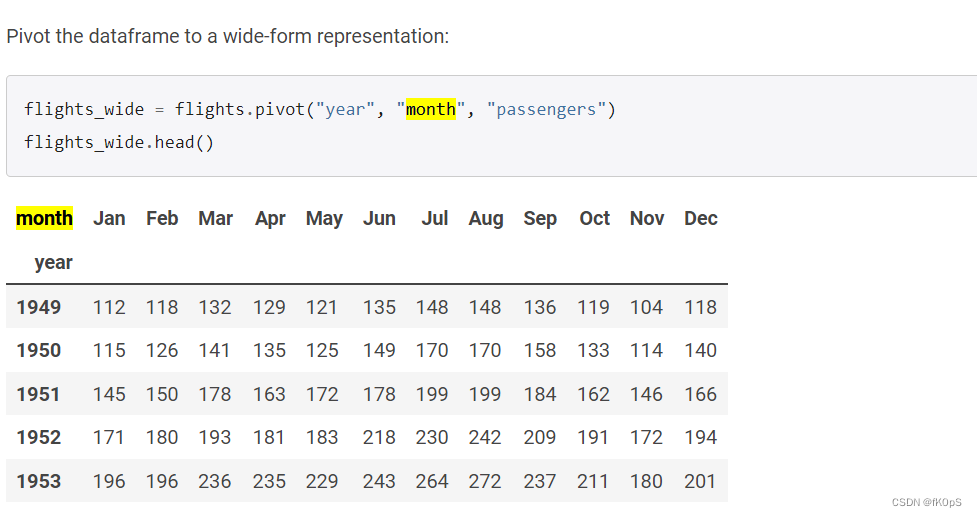

这个阴影部分可以这么理解,1949年,最低的乘客数,最高的乘客数,和平均乘客数;
sns.lineplot(data=flights, x="year", y="passengers") plt.show()
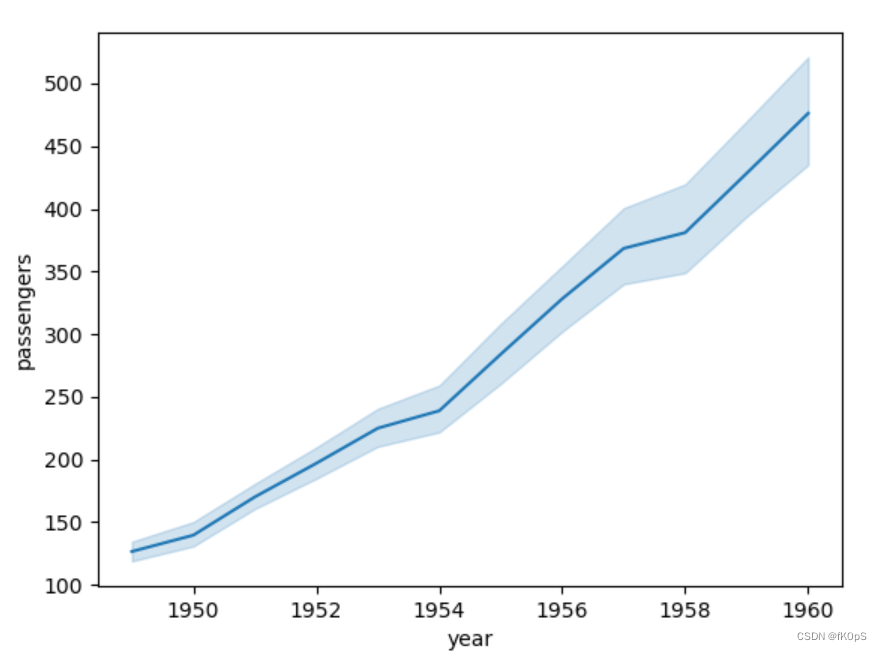
这里有个重要的参数 hue

总结:
问题解决:
def get_dgreeDistr(G):
"""
统计一个图的度分布;
:param G:
:return:
"""
all_k = [G.degree(i) for i in G.nodes()] #获取每个节点的度值;
k = list(set(all_k))
N = len(G.nodes())
Pk = [] #概率分布
for ki in sorted(k):
c = 0
for i in G.nodes():
if G.degree(i) == ki:
c += 1
Pk.append(c/N)
return sorted(k), Pk上边的函数,等价于:
d = dict(nx.degree(net)) x = list(range(max(d.values()) + 1)) # 构造横坐标[1到度最大的值]; y = [i / n for i in nx.degree_histogram(net)] # 分别统计每个度对应的概率;
--------
G1 = nx.barabasi_albert_graph(n, m) # 无标度网络 G2 = nx.barabasi_albert_graph(n, m) # 无标度网络 G3 = nx.barabasi_albert_graph(n, m) # 无标度网络 k1, pk1 = get_dgreeDistr(G1) # k2, pk2 = get_dgreeDistr(G2) # k3, pk3 = get_dgreeDistr(G3) # df1 = pd.DataFrame() df1["k"] = np.array(k1) df1["pk"] = np.array(pk1) df2 = pd.DataFrame() df2["k"] = np.array(k2) df2["pk"] = np.array(pk2) df3 = pd.DataFrame() df3["k"] = np.array(k3) df3["pk"] = np.array(pk3) df = pd.concat([df1, df2, df3],axis =0,ignore_index = True)

================================
求证过程如下:
1、Python如何绘制误差直方图?
2、Python如何绘制曲线的误差图?
3、Python如何绘制曲线的阴影图?