一般来说凸包问题有三种解决方式：蛮力法、Graham-Scan法和分治法。关于蛮力法和分治法的python实现可参考博文：蛮力法、分治法，博主写的很清晰。
这里主要介绍Graham-Scan算法的实现，网上的Graham-Scan算法python实现很多，如这篇博文，原理和实现都很清晰，但是当时使用这个程序测试很大的数据量（如超过1000个点以上）时会报如下错误。
程序报错说栈空，应该是数据点很多的时候多点共线，栈内元素连续弹出，因此基于这篇博文改了一些代码（主要是103行和104行），实现代码如下：
import matplotlib.pyplotas pltimport mathimport timeimport numpyas np
start_t= time.clock()# points中纵坐标最小点的索引，若有多个则返回横坐标最小的点defget_bottom_point(points):
min_index=0
n=len(points)for iinrange(0, n):if points[i][1]< points[min_index][1]or(
points[i][1]== points[min_index][1]and points[i][0]< points[min_index][0]):
min_index= ireturn min_index# 按照与中心点的极角进行排序，余弦，center_point: 中心点defsort_polar_angle_cos(points, center_point):
n=len(points)
cos_value=[]
rank=[]
norm_list=[]for iinrange(0, n):
point_= points[i]
point=[point_[0]- center_point[0], point_[1]- center_point[1]]
rank.append(i)
norm_value= math.sqrt(point[0]* point[0]+ point[1]* point[1])
norm_list.append(norm_value)if norm_value==0:
cos_value.append(1)else:
cos_value.append(point[0]/ norm_value)for iinrange(0, n-1):
index= i+1while index>0:if cos_value[index]> cos_value[index-1]or(
cos_value[index]== cos_value[index-1]and norm_list[index]> norm_list[index-1]):
temp= cos_value[index]
temp_rank= rank[index]
temp_norm= norm_list[index]
cos_value[index]= cos_value[index-1]
rank[index]= rank[index-1]
norm_list[index]= norm_list[index-1]
cos_value[index-1]= temp
rank[index-1]= temp_rank
norm_list[index-1]= temp_norm
index= index-1else:break
sorted_points=[]for iin rank:
sorted_points.append(points[i])return sorted_points# 返回向量与向量[1, 0]之间的夹角-从[1, 0]沿逆时针方向旋转多少度能到达这个向量defvector_angle(vector):
norm_= math.sqrt(vector[0]* vector[0]+ vector[1]* vector[1])if norm_==0:return0
angle= math.acos(vector[0]/ norm_)if vector[1]>=0:return angleelse:return2* math.pi- angle# 两向量的叉乘defcoss_multi(v1, v2):return v1[0]* v2[1]- v1[1]* v2[0]defgraham_scan(points):
bottom_index= get_bottom_point(points)
bottom_point= points.pop(bottom_index)
sorted_points= sort_polar_angle_cos(points, bottom_point)
m=len(sorted_points)if m<2:print("点的数量过少，无法构成凸包")return
stack=[]
stack.append(bottom_point)
stack.append(sorted_points[0])
stack.append(sorted_points[1])# print('当前stack', stack)for iinrange(2, m):
length=len(stack)
top= stack[length-1]
next_top= stack[length-2]
v1=[sorted_points[i][0]- next_top[0], sorted_points[i][1]- next_top[1]]
v2=[top[0]- next_top[0], top[1]- next_top[1]]while coss_multi(v1, v2)>=0:if length<3:# 加上这两行代码之后，数据量很大时不会再报错break# 加上这两行代码之后，数据量很大时不会再报错
stack.pop()
length=len(stack)
top= stack[length-1]
next_top= stack[length-2]
v1=[sorted_points[i][0]- next_top[0], sorted_points[i][1]- next_top[1]]
v2=[top[0]- next_top[0], top[1]- next_top[1]]
stack.append(sorted_points[i])return stack# 产生随机点
n_iter=[100,500,1000,2000,3000]
time_cost=[]for nin n_iter:
points=[]for iinrange(n):
point_x= np.random.randint(1,100)
point_y= np.random.randint(1,100)
temp= np.hstack((point_x, point_y))
point= temp.tolist()
points.append(point)
result= graham_scan(points)# 记录程序运行时间
end_t= time.clock()
time_iter= end_t- start_tprint("Graham-Scan算法运行时间：", time_iter)# draw(list_points, border_line)
time_cost.append(time_iter)# 画结果图"""
for point in points:
plt.scatter(point[0], point[1], marker='o', c='y', s=8)
length = len(result)
for i in range(0, length - 1):
plt.plot([result[i][0], result[i + 1][0]], [result[i][1], result[i + 1][1]], c='r')
plt.plot([result[0][0], result[length - 1][0]], [result[0][1], result[length - 1][1]], c='r')
plt.show()
"""# 不同测试集下的运行时间
plt.plot(n_iter, time_cost)
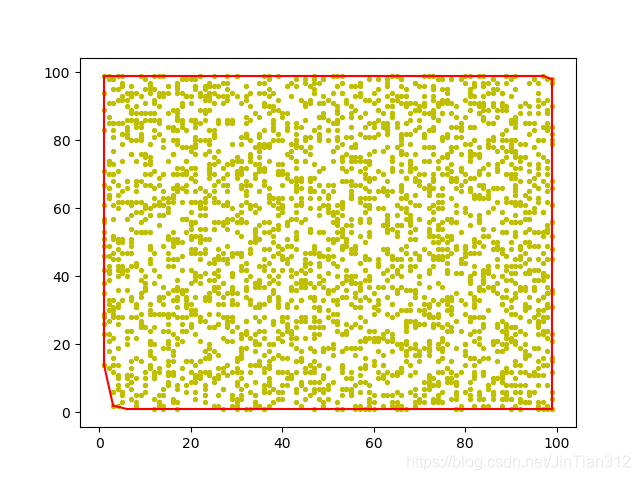
plt.show()运行之后的性能图如下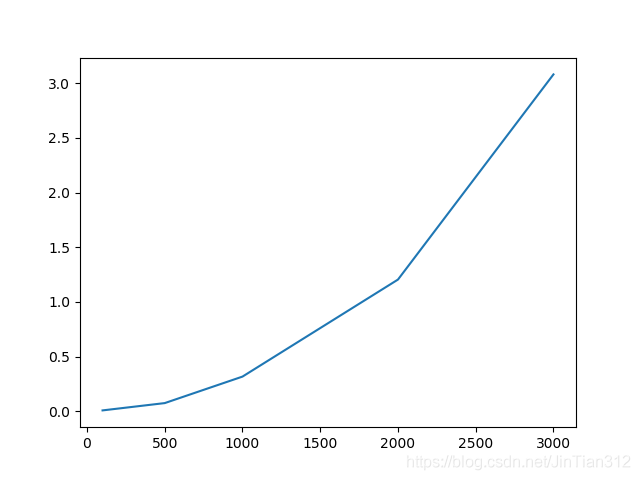
3000个点时返回的凸包如下