二叉树笔记算法笔记汇总

这里汇总的是普通的二叉树常见题型，二叉搜索树等高级二叉树题型单独总结，在后面进行讲解

1. 重建二叉树问题

问题描述：

问题分析1：

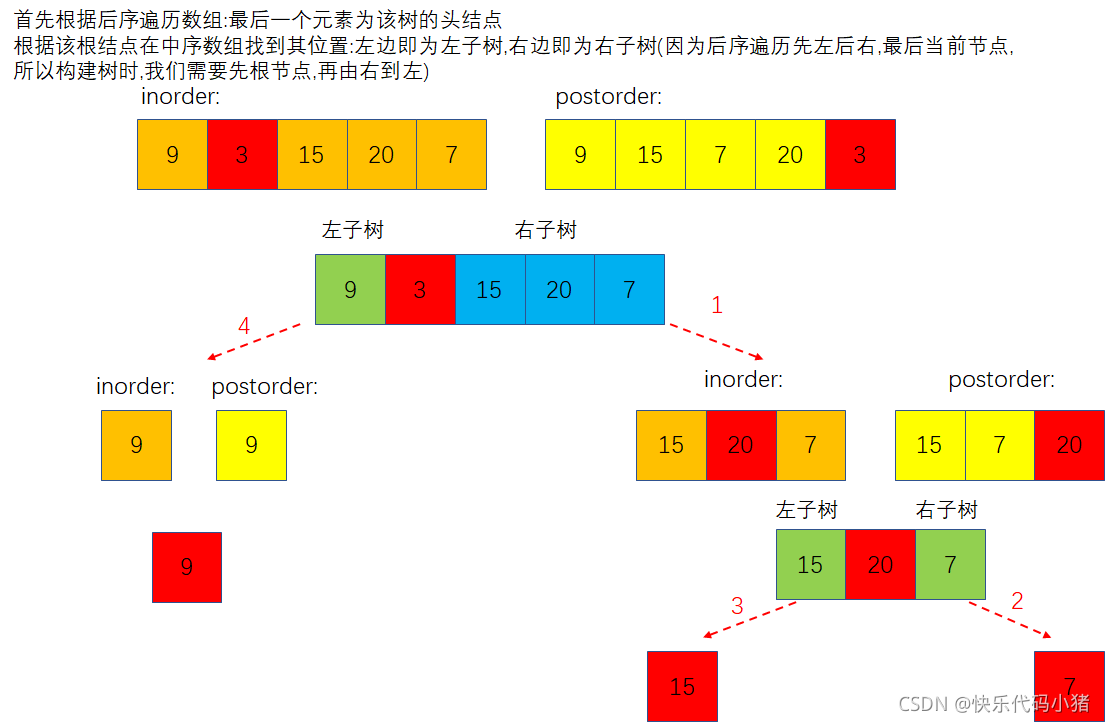
代码实现1：

//定义中序,后序遍历数组属性int[] inorder;int[] postorder;//定义属性post_idx记录每一次的根结点位置int post_idx;//定义一个hashmap:存储中序遍历HashMap<Integer,Integer> idx_map=newHashMap<>();//由中序和后序遍历构建二叉树的实现publicTreeNodebuildTree(int[] inorder,int[] postorder){//将传入的int数组存储到定义的前序和后序数组中this.inorder= inorder;this.postorder= postorder;//根节点即为后序遍历数组的最后一个元素
    post_idx= postorder.length-1;//将中序遍历数组的元素依次加入到idx_map中:key为节点的val值,value为对应中序遍历数组的下标//idx_map:需要保证传入节点的val值都不相同:题设中已经设置你可以假设树中没有重复的元素.int idx=0;for(int val: inorder){
        idx_map.put(val,idx++);}returnhelper(0,inorder.length-1);}privateTreeNodehelper(int in_left,int in_right){//当子树没有节点则返回if(in_left> in_right){returnnull;//即子节点为null}Integer root_val= postorder[post_idx];//取根节点的val值:第一次取的即是整棵树的根节点//根据根节点的val值创建其节点TreeNode root=newTreeNode(root_val);//并在中序遍历数组中获取到根节点的位置Integer root_index= idx_map.get(root_val);//以此位置作为根节点,则中序遍历数组inorder的该位置的左边即为左子树,右边即为右子树//分别递归回溯构建右子树和左子树//注意:因为后序遍历先左后右,最后当前节点,所以构建树时,我们需要先根节点,再由右到左//重点:每一次回溯,post_idx--
    post_idx--;//先递归构建右子树
    root.right=helper(root_index+1,in_right);//再递归构建左子树
    root.left=helper(in_left,root_index-1);//构建完毕,将此时的树的根节点返回return root;}//二叉树的节点类classTreeNode{int val;TreeNode left;TreeNode right;TreeNode(int x){
        val= x;}}

问题分析2：

代码实现2：

//定义前序数组,中序遍历数组属性int[] inorder;int[] preorder;int pre_idx;//定义一个hashmap:存储中序遍历HashMap<Integer,Integer> idx_map=newHashMap<>();//由前序遍历和中序遍历构建二叉树的代码实现publicTreeNodebuildTree(int[] preorder,int[] inorder){this.preorder= preorder;this.inorder= inorder;//第一次根节点的位置即为preorder的第一个位置
    pre_idx=0;//将中序遍历数组的元素依次加入到idx_map中:key为节点的val值,value为对应中序遍历数组的下标//idx_map:需要保证传入节点的val值都不相同:题设中已经设置你可以假设树中没有重复的元素.int idx=0;for(int val: inorder){
        idx_map.put(val,idx++);}returnhelper(0,inorder.length-1);}privateTreeNodehelper(int in_left,int in_right){//当子树没有节点时返回if(in_left> in_right){returnnull;}Integer root_val= preorder[pre_idx];//取根节点的val值:第一次取的即是整棵树的根节点//根据根节点的val创建该根节点TreeNode root=newTreeNode(root_val);//并在中序遍历数组map中找到对应节点的位置Integer root_index= idx_map.get(root_val);//以此位置作为根节点,则中序遍历数组inorder的该位置的左边即为左子树,右边即为右子树//分别递归回溯构建左子树和右子树//注意:因为前序遍历先是根节点,再是从左后右,所以构建树时,我们需要先根节点,再由左到右//重点:每一次回溯,pre_idx++
    pre_idx++;//递归构建左子树
    root.left=helper(in_left,root_index-1);//再递归构建右子树
    root.right=helper(root_index+1,in_right);//将最终树的根节点返回return root;}

2. 二叉树中和为某一值的路径的问题

问题描述：

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和target = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

返回:

[
   [5,4,11,2],
   [5,8,4,5]
]

提示：

1. 节点总数 <= 10000

问题分析：

//实现publicList<List<Integer>>pathSum(TreeNode root,int sum){//定义一个结果集resList<List<Integer>> res=newArrayList<>();//定义一个部分子集List<Integer> sub=newArrayList<>();//通过dfs深度优先遍历完成dfs(root,sum,res,sub);return res;}//dfs实现:privatevoiddfs(TreeNode node,int sum,List<List<Integer>> res,List<Integer> sub){//递归结束的条件if(node==null){//说明此时遍历到该二叉树的叶子节点的下一个节点return;}//将当前节点的val值添加到sub部分子集中
    sub.add(newInteger(node.val));if(node.left==null&& node.right==null){//如果到达叶子节点if(sum== node.val){//当此时sum减到0,则表示此时满足
            res.add(newArrayList<>(sub));}return;}//进行左子树的dfs递归搜索if(node.left!=null){dfs(node.left,sum- node.val,res,sub);//回溯回来记得将sub的最后一个元素去除掉
        sub.remove(sub.size()-1);}//进行右子树的dfs递归搜索if(node.right!=null){dfs(node.right,sum- node.val,res,sub);//回溯回来记得将sub的最后一个元素去除掉
        sub.remove(sub.size()-1);}}

3. 树的子结构

问题描述:

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:

给定的树 A:
     3
    / \
   4   5
  / \
 1   2
给定的树 B:
   4 
  /
 1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

问题分析:

使用递归法进行求解:

• (1)judgeSubStructure(TreeNode A, TreeNode B) 函数：

  终止条件：
  当节点 B 为空：说明树 B已匹配完成（越过叶子节点），因此返回 true；
  当节点 A为空：说明已经越过树 A叶子节点，即匹配失败，返回 false ；
  当节点 A和 B 的值不同：说明匹配失败，返回 false ；
  返回值：
  判断 A和 B的左子节点是否相等，即 judgeSubStructure(A.left, B.left) ；
  判断 AA 和 BB 的右子节点是否相等，即 judgeSubStructure(A.right, B.right) ；

• (2)isSubStructure(A, B) 函数：

  特例处理： 当 树 A 为空 或 树 B 为空 时，直接返回 false ；
  返回值： 若树 B 是树 A 的子结构，则必满足以下三种情况之一，因此用或 || 连接；
  以 节点 A 为根节点的子树 包含树 B ，对应 judgeSubStructure(A, B)；
  树 B 是 树 A左子树 的子结构，对应 isSubStructure(A.left, B)；
  树 B 是 树 A右子树 的子结构，对应 isSubStructure(A.right, B)；

java代码实现:

publicbooleanisSubStructure(TreeNodeA,TreeNodeB){//递归条件A != null && B != nullreturn(A!=null&&B!=null)&&(judgeSubStructure(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B));}privatebooleanjudgeSubStructure(TreeNodeA,TreeNodeB){if(B==null){//B树匹配到末尾,则表示A树种存在该B树子结构,返回truereturntrue;}elseif(A==null){//遍历到A树的一端末尾仍未发现匹配,则返回falsereturnfalse;}//若A树当前结点的val值 != B树当前结点的val值,则直接返回false,表示此时的A子树不是B树结构if(A.val!=B.val){returnfalse;}//递归比较A树的左节点和B树的左节点以及A树的右节点和B树的右节点returnjudgeSubStructure(A.left,B.left)&&judgeSubStructure(A.right,B.right);}

JavaScript代码实现:

varisSubStructure=function(A,B){return(A!=null&&B!=null)&&(judgeSubStructor(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B));};varjudgeSubStructor=function(A,B){//结束条件：如果B遍历结束说明匹配，如果A遍历结束说明不匹配if(B==null){returntrue;}elseif(A==null){returnfalse;}if(A.val!=B.val){returnfalse;}//如果当前的两个值相等，则判断A,B两树的左子树与右子树是否相等returnjudgeSubStructor(A.left,B.left)&&judgeSubStructor(A.right,B.right);}

4. 二叉树的镜像

问题描述:

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

镜像输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

限制：

0 <= 节点个数 <= 1000

java代码实现:

也可以使用栈，对每一个节点都进行左右节点的交换

publicTreeNodemirrorTree(TreeNode root){if(root==null){return root;}TreeNode temp= root.left;
    root.left= root.right;
    root.right= temp;mirrorTree(root.left);mirrorTree(root.right);return root;}

JavaScript代码实现:

方法一：varmirrorTree=function(root){//特殊情况if(root==null){return root;}//否则交换左右子树let temp= root.left;
    root.left= root.right;
    root.right= temp;//左右子树分别进行交换mirrorTree(root.left)mirrorTree(root.right)return root;};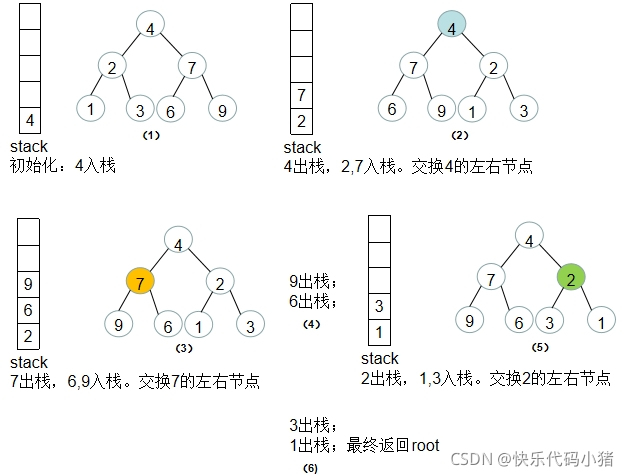

方法二：varmirrorTree=function(root){if(root==null)returnnull;let stack=[root];while(stack.length){let temp= stack.pop();if(temp.left!=null){
            stack.push(temp.left);}if(temp.right!=null){
            stack.push(temp.right)}let t= temp.left;
        temp.left= temp.right;
        temp.right= t;}return root;}

5. 判断对称的二叉树

问题描述:

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

示例 1:

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

限制：

0 <= 节点个数 <= 1000

问题分析:

使用递归法进行求解:

如果一个二叉树是对称的,即表示该二叉树的左子树和右子树是完全一致的

我们即可以使用递归反进行实现,如果当前根节点的左子树的val值等于右子树的val值,那么我们递归比较该左子树的左子树和右子树的右子树以及左子树的右子树和右子树的左子树;

如果比较过程中,left和right均为null: 则直接返回true; 如果只有一方为null,则一定不是对称的,直接返回false;

java代码实现:

publicbooleanisSymmetric(TreeNode root){//如果该二叉树为空或者只有一个根节点，直接返回trueif(root==null||(root.left==null&& root.right==null)){returntrue;}//否则我们调用judge函数进行判断returnjudge(root.left,root.right);}privatebooleanjudge(TreeNode left,TreeNode right){if(left==null&& right==null){returntrue;}if(left==null|| right==null|| left.val!= right.val){returnfalse;}returnjudge(left.left,right.right)&&judge(left.right,right.left);}}

JavaScript代码实现:

/**
	两棵子树进行比较
**/varisSymmetric=function(root){if(root==null)returntrue;returnisMirror(root.left, root.right);};functionisMirror(r1, r2){if(r1==null&& r2==null){returntrue;}if(r1==null|| r2==null){returnfalse;}return r1.val== r2.val&&isMirror(r1.left, r2.right)&&isMirror(r1.right, r2.left);}

6. 从上到下打印二叉树

问题描述:

6 - I. 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树:[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回：

[3,9,20,15,7]

提示：

1. 节点总数 <= 1000

问题分析:

这是典型的二叉树的BFS求解问题:

特例处理： 当树的根节点为空，则直接返回空列表 [ ] ；
BFS 循环： 我们定义一个队列nodes,初始化将根节点root节点加入到nodes队列中,循环结束条件[nodes为空]
出队： 队首元素出队，记为 temp；
添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 nodes,并将左右子节点的val值加入到list集合中 ；
返回值： 定义一个结果集res(大小即为list集合的大小),将list集合的结果拷贝到res中,最后返回打印结果列表 res 即可

java代码实现:

//使用BFS进行求解publicint[]levelOrder(TreeNode root){if(root==null)//如果root节点为null,则直接返回空的数组结果集returnnewint[0];//定义一个list集合:存储每一层顺序遍历的节点的val值List<Integer> list=newLinkedList<>();//定义nodes:存储节点LinkedList<TreeNode> nodes=newLinkedList<>();
    list.add(root.val);//我们首先将第一层,即root节点的val值加入到集合中
    nodes.add(root);while(!nodes.isEmpty()){TreeNode temp= nodes.removeFirst();if(temp.left!=null){
            list.add(temp.left.val);
            nodes.add(temp.left);}if(temp.right!=null){
            list.add(temp.right.val);
            nodes.add(temp.right);