分离链接法
解决冲突的第一种方法通常叫作分离链接法（separate chaining），其做法是将散列到同一个值的所有元素保留在一个表中。为方便起见这些表都有表头。如果空间很紧，则更可取的方法是避免使用这些表头。（分离链接法，个人认为是位置和位置之间分离处理，将散列到同一位置的元素用表链接起来，而不是去寻找新的位置，与开放定址法相对）
为执行Find，我们使用散列函数来确定究竟考察哪个表。此时我们以通常的方式遍历该表并返回所找到的被查找项所在位置。为执行Insert，我们遍历一个相应的表以检查该元素是否已经处在适当的位置（如果要插入重复元，那么通常要留出一个额外的域，这个域当重复元出现时增1）。如果这个元素是新的元素，那么插入到表的前端，或者插入到表的末尾，哪个容易就执行哪个。有时将新元素插入到表的前端不仅因为方便，而且还因为新近插入的元素最有可能最先被访问。
类型声明：
#define MinSize (10)
typedef unsigned int Index;
typedef struct HashTbl* HashTable;
typedef struct ListNode* PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
typedef int ElementType;
struct HashTbl
{
int tableSize;
List* theLists;
};
struct ListNode
{
ElementType element;
Position next;
};初始化：
第8行可以改进，自定义一个函数NextPrime，用于找到并返回Size的下一个素数。然后我们把这个素数用作实际表大小赋值给h->tableSize。
HashTable InitializeTable(int tableSize)
{
int i;
//Allocate table
HashTable h = (HashTable)malloc(sizeof(struct HashTbl));
if (h == NULL)
return NULL;
h->tableSize = tableSize > MinSize ? tableSize : MinSize;
//Allocate array of lists
h->theLists = (List*)malloc(h->tableSize * sizeof(List));
if (h->theLists == NULL)
FatalError("out of space");
//Allocate list headers
for (i = 0; i < h->tableSize; i++)
{
h->theLists[i] = (PtrToNode)malloc(sizeof(struct ListNode));
if (h->theLists[i] == NULL)
{
FatalError("out of space!");
}
else
h->theLists[i]->next = NULL;
}
return h;
}散列函数、查找与检索：
这里直接用的简单的散列函数，查找例程中的第十行有必要说明一下，它的循环是找到表的末尾即NULL处停止，或者找到不为NULL，且节点的元素值与关键字值相等时停止。所以没找到key时，tmpNode会返回NULL，找到了返回元素值与key相等的节点的地址。（为简单起见我们这里的元素值和关键字都为int，一般来说还可能为字符串，字符串的比较就需要用到strcmp）
检索例程中检索错误我是用返回 INT_MAX表示，但是实际上应该写成报错。
Index Hash(HashTable h, ElementType key)
{
return key % h->tableSize;
}
Position Find(HashTable h, ElementType key)
{
if (h == NULL)
return NULL;
unsigned int index = Hash(h, key);
Position tmpNode = h->theLists[index]->next;
while (tmpNode != NULL && tmpNode->element != key)
tmpNode = tmpNode->next;
return tmpNode;
}
ElementType Retrieve(Position p)
{
if (p != NULL)
return p->element;
else
return INT_MAX;
}插入：
如果要插入的项已经存在，那么我们就什么也不做，否则我们把它放到表的前端。tmpNode的值可以通过直接调用Find函数得到，但是这样的话就会多一次散列函数的运算，如果散列函数构成了程序运行时间的重要部分，就应该避免多次计算。
void Insert(HashTable h, ElementType key)
{
if (h == NULL)
return;
unsigned int index = Hash(h, key);
List L = h->theLists[index];
Position tmpNode = L->next;
while (tmpNode != NULL & tmpNode->element != key)
tmpNode = tmpNode->next;
if (tmpNode == NULL)
{
tmpNode = (PtrToNode)malloc(sizeof(struct ListNode));
if (tmpNode == NULL)
{
printf("out of space");
return;
}
else
{
tmpNode->element = key;
tmpNode->next = L->next;
L->next = tmpNode;
}
}
}删除：
void Delete(HashTable h, ElementType key)
{
if (h == NULL)
return;
unsigned int index = Hash(h, key);
Position prevNode = h->theLists[index];
Position tmpNode = prevNode->next;
while (tmpNode != NULL && tmpNode->element != key)
{
prevNode = tmpNode;
tmpNode = tmpNode->next;
}
//Key was found
if (tmpNode != NULL)
{
prevNode->next = tmpNode->next;
free(tmpNode);
}
}销毁表：
此例程编写需要格外仔细，稍不注意就可能释放不完全而导致内存泄漏。
void DestroyTable(HashTable h)
{
if (h == NULL)
return;
int i;
Position tmpNode, nextNode;
for (i = 0; i < h->tableSize; i++)
{
tmpNode = h->theLists[i];
while (tmpNode != NULL)
{
nextNode = tmpNode->next;
free(tmpNode);
tmpNode = nextNode;
}
}
free(h->theLists);
free(h);
} 我们定义散列表的装填因子（load factor）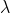
为散列表中的元素个数与散列表大小的比值。表的平均长度为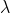。执行一次查找所需要的工作是计算散列函数值所需要的常数时间加上遍历表所用的时间。在一次不超过的查找中，遍历的链接数平均为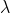（不包含最后的NULL链接）。成功的查找则需要遍历大约；它保证必然会遍历一个链接（因为查找是成功的），而我们也期望沿着一个表中途就能找到匹配的元素。这就指出，表的大小实际上并不重要，而装填因子才是重要的。分离链接散列的一般法则是使得表的大小尽量与预料的元素个数差不多（换句话说，让
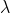≈1）。正如前面提到的，使表的大小是素数以保证一个好的分布，这也是一个好的想法