一、算法步骤

1. 首先找到点集中y坐标最小的点作为初始点$p_0$，若y坐标相同，选取x坐标最小的一个点作为$p_0$
2. 以p0为原点，对点集进行极角排序得到集合 { p 0 , p 1 . . . p n } \left\{p_0,p_1...p_n\right\}{p0,p1...pn}
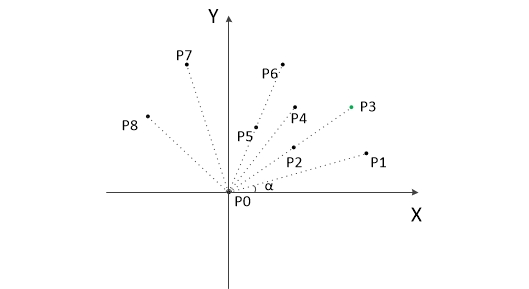
3. 令i=1,构建一个存储凸包边界的栈stack，栈内初始存储元素$p_0$与$p_1$
4. 判断集合下一个元素$p_{i+1}$在栈顶两元素构成的向量的哪一侧：
      若在左侧，则点$p_{i+1}$进栈，$i=i+1;$重复执行步骤3，直至$i>n$
      若在右侧，则栈顶元素出栈，重复执行步骤3

二、算法示意图

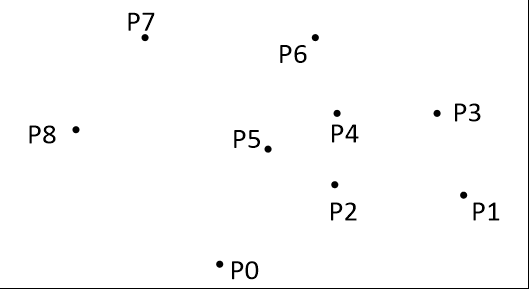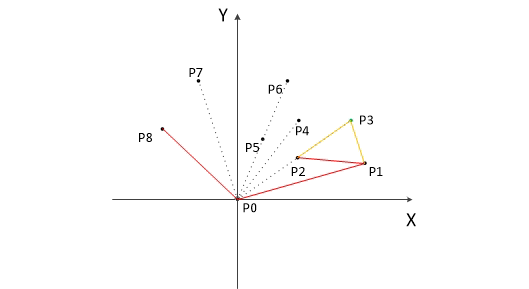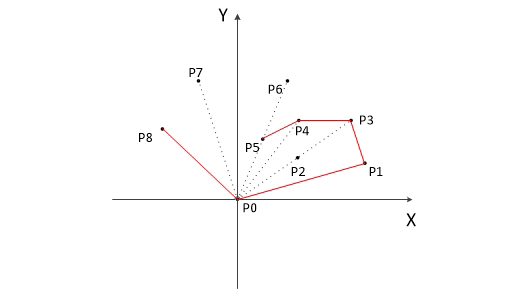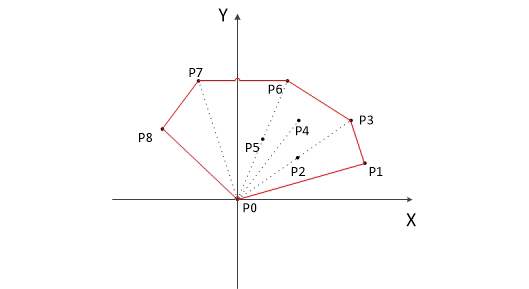
三、代码

1.导入python库

from math import atan2
import math
import matplotlib.pyplot as plt
import numpy as np

2.构造工具函数

defatan(point,y,x):'''返回点(x,y)相对于point的角度'''
    x= x- point[0]
    y= y- point[1]if x==0and y==0:return0
    point=(5,0)#表示x轴的向量，随便取
    cos=(point[0]*x+point[1]*y)/(math.sqrt(point[0]**2+point[1]**2)*math.sqrt(x**2+y**2))return np.arccos(cos)*(180/math.pi)

defangle_sort(p0,points):'''对点集从小到大进行极角排序'''
    dic={}for pointin points:
        angle= atan(p0,point[1],point[0])
        dic[point]= angle
    points=[k[0]for kin sorted(dic.items(),key=lambda x:x[1])]#,reverse=Truereturn points

defcross_product(a,b,c):'''判断点c在由点a,b构成的向量的那一侧'''
    result= a[0]*b[1]-a[1]*b[0]+ b[0]*c[1]-b[1]*c[0]+ c[0]*a[1]-c[1]*a[0]if result<0:returnFalse#点c在向量ab右边 返回Falseelse:returnTrue#点c在向量ab左边  返回True

3.初始化点集

集合的高度由vertical决定，宽度由level决定

key=3
num=120
level=10
vertical=5
seed= np.random.RandomState(key)
seed2= np.random.RandomState(key+1)Z1= seed.rand(num,1)*level#生成点集Z2= seed2.rand(num,1)*verticalZ= np.concatenate([Z1,Z2],axis=1)
points=[tuple(i)for iinZ]

三、计算凸包

#起点为y坐标最小的点
ymin= min(points,key=lambda x:x[0])[1]
start= min([ifor iin pointsif i[1]== ymin],key= lambda x:x[0])
stack=[]#定义栈
points= angle_sort(start,points)
stack.append(points[0])
stack.append(points[1])
i=2while len(stack)!=0and i!= len(points):if cross_product(stack[len(stack)-2],stack[len(stack)-1],points[i]):
        stack.append(points[i])
        i+=1else:
        stack.pop()if len(stack)<2:
            stack.append(points[i])
            i+=1
        continue

四、画出凸包

stack.append(stack[0])
x=[i[0]for iin points]
y=[i[1]for iin points]
x0=[i[0]for iin stack]
y0=[i[1]for iin stack]
plt.figure(figsize=(10,10))
plt.scatter(x,y)
plt.plot(x0,y0)

plt.xlim(-1,11)
plt.ylim(-1,6)
i=0for a,bin zip(x,y):
    plt.text(a, b, i)
    i+=1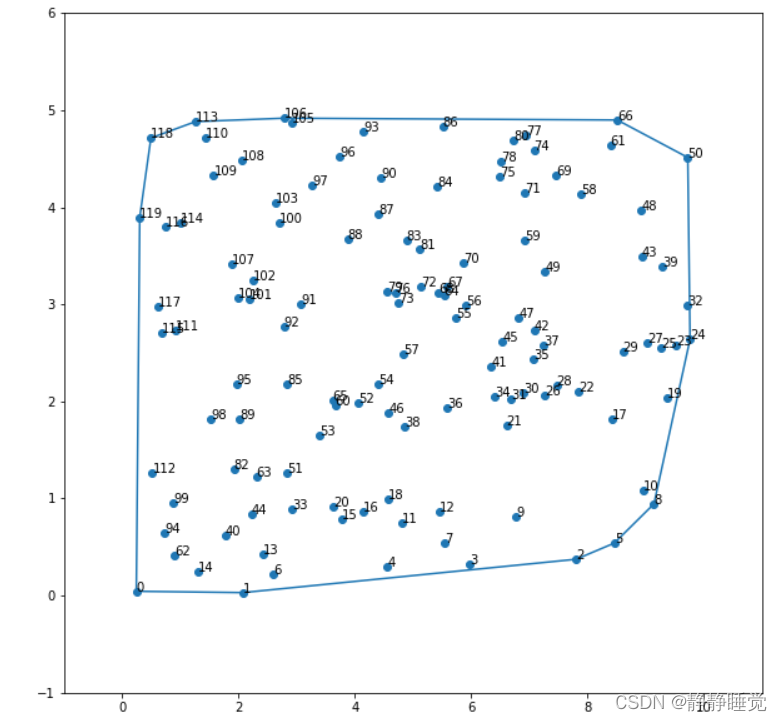

该算法参考自算法导论第33章凸包的生成