一、CART决策树算法简介
CART(Classification And Regression Trees 分类回归树)算法是一种树构建算法,既可以用于分类任务,又可以用于回归。相比于 ID3 和 C4.5 只能用于离散型数据且只能用于分类任务,CART 算法的适用面要广得多,既可用于离散型数据,又可以处理连续型数据,并且分类和回归任务都能处理。
本文仅讨论基本的CART分类决策树构建,不讨论回归树和剪枝等问题。
首先,我们要明确以下几点:
1. CART算法是二分类常用的方法,由CART算法生成的决策树是二叉树,而 ID3 以及 C4.5 算法生成的决策树是多叉树,从运行效率角度考虑,二叉树模型会比多叉树运算效率高。
2. CART算法通过基尼(Gini)指数来选择最优特征。
二、基尼系数
基尼系数代表模型的不纯度,基尼系数越小,则不纯度越低,注意这和 C4.5的信息增益比的定义恰好相反。
分类问题中,假设有K个类,样本点属于第k类的概率为pk,则概率分布的基尼系数定义为: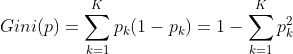
若CART用于二类分类问题(不是只能用于二分类),那么概率分布的基尼系数可简化为
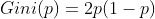
假设使用特征 A 将数据集 D 划分为两部分 D1 和 D2,此时按照特征 A 划分的数据集的基尼系数为: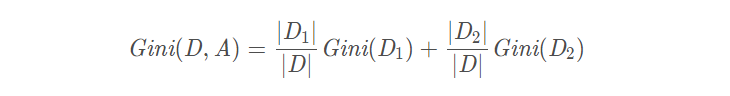
三、CART决策树生成算法
输入:训练数据集D,停止计算的条件
输出:CART决策树
根据训练数据集,从根结点开始,递归地对每个结点进行以下操作,构建二叉决策树:
(1)计算现有特征对该数据集的基尼指数,如上面所示;
(2)选择基尼指数最小的值对应的特征为最优特征,对应的切分点为最优切分点(若最小值对应的特征或切分点有多个,随便取一个即可);
(3)按照最优特征和最优切分点,从现结点生成两个子结点,将训练数据集中的数据按特征和属性分配到两个子结点中;
(4)对两个子结点递归地调用(1)(2)(3),直至满足停止条件。
(5)生成CART树。
算法停止的条件:结点中的样本个数小于预定阈值,或样本集的基尼指数小于预定阈值(样本基本属于同一类,如完全属于同一类则为0),或者特征集为空。
注:最优切分点是将当前样本下分为两类(因为我们要构造二叉树)的必要条件。对于离散的情况,最优切分点是当前最优特征的某个取值;对于连续的情况,最优切分点可以是某个具体的数值。具体应用时需要遍历所有可能的最优切分点取值去找到我们需要的最优切分点。
四、CART算法的Python实现
from math import log
# 构造数据集
def create_dataset():
dataset = [['youth', 'no', 'no', 'just so-so', 'no'],
['youth', 'no', 'no', 'good', 'no'],
['youth', 'yes', 'no', 'good', 'yes'],
['youth', 'yes', 'yes', 'just so-so', 'yes'],
['youth', 'no', 'no', 'just so-so', 'no'],
['midlife', 'no', 'no', 'just so-so', 'no'],
['midlife', 'no', 'no', 'good', 'no'],
['midlife', 'yes', 'yes', 'good', 'yes'],
['midlife', 'no', 'yes', 'great', 'yes'],
['midlife', 'no', 'yes', 'great', 'yes'],
['geriatric', 'no', 'yes', 'great', 'yes'],
['geriatric', 'no', 'yes', 'good', 'yes'],
['geriatric', 'yes', 'no', 'good', 'yes'],
['geriatric', 'yes', 'no', 'great', 'yes'],
['geriatric', 'no', 'no', 'just so-so', 'no']]
features = ['age', 'work', 'house', 'credit']
return dataset, features
# 计算当前集合的Gini系数
def calcGini(dataset):
# 求总样本数
num_of_examples = len(dataset)
labelCnt = {}
# 遍历整个样本集合
for example in dataset:
# 当前样本的标签值是该列表的最后一个元素
currentLabel = example[-1]
# 统计每个标签各出现了几次
if currentLabel not in labelCnt.keys():
labelCnt[currentLabel] = 0
labelCnt[currentLabel] += 1
# 得到了当前集合中每个标签的样本个数后,计算它们的p值
for key in labelCnt:
labelCnt[key] /= num_of_examples
labelCnt[key] = labelCnt[key] * labelCnt[key]
# 计算Gini系数
Gini = 1 - sum(labelCnt.values())
return Gini
# 提取子集合
# 功能:从dataSet中先找到所有第axis个标签值 = value的样本
# 然后将这些样本删去第axis个标签值,再全部提取出来成为一个新的样本集
def create_sub_dataset(dataset, index, value):
sub_dataset = []
for example in dataset:
current_list = []
if example[index] == value:
current_list = example[:index]
current_list.extend(example[index + 1 :])
sub_dataset.append(current_list)
return sub_dataset
# 将当前样本集分割成特征i取值为value的一部分和取值不为value的一部分(二分)
def split_dataset(dataset, index, value):
sub_dataset1 = []
sub_dataset2 = []
for example in dataset:
current_list = []
if example[index] == value:
current_list = example[:index]
current_list.extend(example[index + 1 :])
sub_dataset1.append(current_list)
else:
current_list = example[:index]
current_list.extend(example[index + 1 :])
sub_dataset2.append(current_list)
return sub_dataset1, sub_dataset2
def choose_best_feature(dataset):
# 特征总数
numFeatures = len(dataset[0]) - 1
# 当只有一个特征时
if numFeatures == 1:
return 0
# 初始化最佳基尼系数
bestGini = 1
# 初始化最优特征
index_of_best_feature = -1
# 遍历所有特征,寻找最优特征和该特征下的最优切分点
for i in range(numFeatures):
# 去重,每个属性值唯一
uniqueVals = set(example[i] for example in dataset)
# Gini字典中的每个值代表以该值对应的键作为切分点对当前集合进行划分后的Gini系数
Gini = {}
# 对于当前特征的每个取值
for value in uniqueVals:
# 先求由该值进行划分得到的两个子集
sub_dataset1, sub_dataset2 = split_dataset(dataset,i,value)
# 求两个子集占原集合的比例系数prob1 prob2
prob1 = len(sub_dataset1) / float(len(dataset))
prob2 = len(sub_dataset2) / float(len(dataset))
# 计算子集1的Gini系数
Gini_of_sub_dataset1 = calcGini(sub_dataset1)
# 计算子集2的Gini系数
Gini_of_sub_dataset2 = calcGini(sub_dataset2)
# 计算由当前最优切分点划分后的最终Gini系数
Gini[value] = prob1 * Gini_of_sub_dataset1 + prob2 * Gini_of_sub_dataset2
# 更新最优特征和最优切分点
if Gini[value] < bestGini:
bestGini = Gini[value]
index_of_best_feature = i
best_split_point = value
return index_of_best_feature, best_split_point
# 返回具有最多样本数的那个标签的值('yes' or 'no')
def find_label(classList):
# 初始化统计各标签次数的字典
# 键为各标签,对应的值为标签出现的次数
labelCnt = {}
for key in classList:
if key not in labelCnt.keys():
labelCnt[key] = 0
labelCnt[key] += 1
# 将classCount按值降序排列
# 例如:sorted_labelCnt = {'yes': 9, 'no': 6}
sorted_labelCnt = sorted(labelCnt.items(), key = lambda a:a[1], reverse = True)
# 下面这种写法有问题
# sortedClassCount = sorted(labelCnt.iteritems(), key=operator.itemgetter(1), reverse=True)
# 取sorted_labelCnt中第一个元素中的第一个值,即为所求
return sorted_labelCnt[0][0]
def create_decision_tree(dataset, features):
# 求出训练集所有样本的标签
# 对于初始数据集,其label_list = ['no', 'no', 'yes', 'yes', 'no', 'no', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
label_list = [example[-1] for example in dataset]
# 先写两个递归结束的情况:
# 若当前集合的所有样本标签相等(即样本已被分“纯”)
# 则直接返回该标签值作为一个叶子节点
if label_list.count(label_list[0]) == len(label_list):
return label_list[0]
# 若训练集的所有特征都被使用完毕,当前无可用特征,但样本仍未被分“纯”
# 则返回所含样本最多的标签作为结果
if len(dataset[0]) == 1:
return find_label(label_list)
# 下面是正式建树的过程
# 选取进行分支的最佳特征的下标和最佳切分点
index_of_best_feature, best_split_point = choose_best_feature(dataset)
# 得到最佳特征
best_feature = features[index_of_best_feature]
# 初始化决策树
decision_tree = {best_feature: {}}
# 使用过当前最佳特征后将其删去
del(features[index_of_best_feature])
# 子特征 = 当前特征(因为刚才已经删去了用过的特征)
sub_labels = features[:]
# 递归调用create_decision_tree去生成新节点
# 生成由最优切分点划分出来的二分子集
sub_dataset1, sub_dataset2 = split_dataset(dataset,index_of_best_feature,best_split_point)
# 构造左子树
decision_tree[best_feature][best_split_point] = create_decision_tree(sub_dataset1, sub_labels)
# 构造右子树
decision_tree[best_feature]['others'] = create_decision_tree(sub_dataset2, sub_labels)
return decision_tree
# 用上面训练好的决策树对新样本分类
def classify(decision_tree, features, test_example):
# 根节点代表的属性
first_feature = list(decision_tree.keys())[0]
# second_dict是第一个分类属性的值(也是字典)
second_dict = decision_tree[first_feature]
# 树根代表的属性,所在属性标签中的位置,即第几个属性
index_of_first_feature = features.index(first_feature)
# 对于second_dict中的每一个key
for key in second_dict.keys():
# 不等于'others'的key
if key != 'others':
if test_example[index_of_first_feature] == key:
# 若当前second_dict的key的value是一个字典
if type(second_dict[key]).__name__ == 'dict':
# 则需要递归查询
classLabel = classify(second_dict[key], features, test_example)
# 若当前second_dict的key的value是一个单独的值
else:
# 则就是要找的标签值
classLabel = second_dict[key]
# 如果测试样本在当前特征的取值不等于key,就说明它在当前特征的取值属于'others'
else:
# 如果second_dict['others']的值是个字符串,则直接输出
if isinstance(second_dict['others'],str):
classLabel = second_dict['others']
# 如果second_dict['others']的值是个字典,则递归查询
else:
classLabel = classify(second_dict['others'], features, test_example)
return classLabel
if __name__ == '__main__':
dataset, features = create_dataset()
decision_tree = create_decision_tree(dataset, features)
# 打印生成的决策树
print(decision_tree)
# 对新样本进行分类测试
features = ['age', 'work', 'house', 'credit']
test_example = ['midlife', 'yes', 'no', 'great']
print(classify(decision_tree, features, test_example))
若是二分类问题,则函数calcGini和choose_best_feature可简化如下:
# 计算样本属于第1个类的概率p
def calcProbabilityEnt(dataset):
numEntries = len(dataset)
count = 0
label = dataset[0][len(dataset[0]) - 1]
for example in dataset:
if example[-1] == label:
count += 1
probabilityEnt = float(count) / numEntries
return probabilityEnt
def choose_best_feature(dataset):
# 特征总数
numFeatures = len(dataset[0]) - 1
# 当只有一个特征时
if numFeatures == 1:
return 0
# 初始化最佳基尼系数
bestGini = 1
# 初始化最优特征
index_of_best_feature = -1
for i in range(numFeatures):
# 去重,每个属性值唯一
uniqueVals = set(example[i] for example in dataset)
# 定义特征的值的基尼系数
Gini = {}
for value in uniqueVals:
sub_dataset1, sub_dataset2 = split_dataset(dataset,i,value)
prob1 = len(sub_dataset1) / float(len(dataset))
prob2 = len(sub_dataset2) / float(len(dataset))
probabilityEnt1 = calcProbabilityEnt(sub_dataset1)
probabilityEnt2 = calcProbabilityEnt(sub_dataset2)
Gini[value] = prob1 * 2 * probabilityEnt1 * (1 - probabilityEnt1) + prob2 * 2 * probabilityEnt2 * (1 - probabilityEnt2)
if Gini[value] < bestGini:
bestGini = Gini[value]
index_of_best_feature = i
best_split_point = value
return index_of_best_feature, best_split_point
五、运行结果
