- 线性表简介
- 面试题总体分析
- 一些例题:
- 例一:元素出入栈顺序合法性判断
- 例二:两个队列实现一个堆栈
- 例三:两个堆栈实现一个队列
- 例四:支持查询最小值的堆栈
- 例五:单调堆栈–最大直方图
- 例六:单调队列–滑动窗口最大值
- 总结
1. 线性表简介
- 堆栈和队列统称为线性表
- 简单的线性表
- 数组和链表可以实现的两种数据结构
- 堆栈
- 后进先出(Last In First Out)
- DFS思想
- 队列
- 先进先出(First In First Out)
- BFS思想
2. 标示题总体分析
- 堆栈
- 基本理解
- DFS
- 深度优先–按照深度遍历
- 递归转非递归
- 队列
- 基本理解
- BFS
- 广度优先–按照层序遍历
3. 例题
1. 元素出入栈顺序合法性判断
- 给定一些元素的入栈顺序和出栈顺序,问是否可能?(假设所有元素都不相同)
- 分析:模拟堆栈即可,如果当前要出栈的元素恰好在栈顶,则必须出栈,否则入栈。
def is_valid(nums_in, nums_out):
"""
总体时间复杂度为是线性,进行的核心操作append 和pop是线性复杂度
时间复杂度O(n)
空间复杂度O(n): 只需要引入一个辅助栈
"""
# 判断入栈大小和出栈大小一致
assert len(nums_in) == len(nums_out)
# 建立辅助栈
stack = []
n = len(nums_out)
j = 0
# 遍历每一个出栈元素
for i in range(n):
# 如果栈是空或者栈顶元素不是当前出栈元素,不断进行操作
while not stack or stack[-1] != nums_out[i]:
if j >= len(nums_in):
return False
else:
# 先入栈,然后模拟出栈
stack.append(nums_in[j])
j += 1
# 相等的时候,必须出栈。
stack.pop(-1)
return True
test_in = [1, 2, 3, 4, 5]
test_out = [1, 5, 3, 2, 4]
print(is_valid(test_in, test_out))
2. 用两个队列实现一个堆栈
- 队列无论怎么操作,元素顺序不会改变
- 连个队列来回倒,保证一个队列时空的,用空队列临时存储除队尾外的所有元素
例如q1非空,q2是空的,此时需要出栈。实际上要出的是q1里面的最后一个元素,我们把q1里面元素一个一个放入q2里面(所有元素顺序不会变化),直到剩下一个,再让它出队列即可;
def queue_mimic_stack(nums, ops='pop_'):
"""
空间复杂度:O(n)
时间复杂度:O(n^2)
"""
queue1, queue2 = [], []
ret = [] # 出栈元素存储
def push(nums):
nonlocal queue1, queue2
# 始终维护一个空队列
for ele in nums:
if not queue1: queue1.append(ele)
else: queue2.append(ele)
return None
def pop_():
nonlocal ret, queue1, queue2
for ele in nums:
# 输入队列中的元素入栈
queue1.append(ele)
while queue1 or queue2:
for i in range(len(queue1)-1):
tmp = queue1.pop(0)
queue2.append(tmp)
cur = queue1.pop(0)
ret.append(cur)
# 回忆BFS中两个队列交换顺序
queue1, queue2 = queue2, queue1
if ops == 'pop_':
pop_()
else:
push()
return ret
print(queue_mimic_stack([3, 2, 4, 5]))
用两个堆栈实现一个队列
- S1负责入队,S2负责出队[翻两下变正向]
- 入队直接入到S1里面
- 要出队如果S2非空,则先从S2出,否则把S1里面的元素全部压入S2中
- 理解
- S1负责存放入队元素
- S2负责出队并反向
- 每个元素实际上反向了两次,出入一次S1,出入一次S2
class StackMimicQueue():
def __init__(self):
"""
其中stack1负责入队列
stack2负责出队列
"""
self.__stack1 = []
self.__stack2 = []
def enqueue(self, num):
self.__stack1.append(num)
def dequeue(self):
"""时间复杂度为O(4*n)=O(n)"""
if self.__stack2:
tmp = self.__stack2.pop(-1)
return tmp
else:
while self.__stack1:
tmp = self.__stack1.pop(-1)
self.__stack2.append(tmp)
tmp = self.__stack2.pop(-1)
return tmp
return None
smq = StackMimicQueue()
test = [2, 3, 4, 5]
for ele in test:
smq.enqueue(ele)
smq.dequeue()
例4 支持查找最小元素的堆栈
- 一个堆栈除了支持push, pop以外还要支持一个操作getMin得到当前堆栈里面所有元素的最小值
- 方法1:
- 用两个堆栈,S1和S2,s1正常使用,S2一直空着
- get_min的时候,把S1中的元素一个一个弹到S2中,每弹出一个,顺便求当前的最小值,然后在从S2把元素一个一个弹回到s1,也清空了S2;
- 方法二
- 用两个堆栈,s1维护原来的值,s2维护最小值,它们元素个数一样多。
- 方法三:
- S2真的需要存储那么多元素么?假设之前入过一个最小值,S2的顶端存了许多相同的最小值。
- 方法1:
class MinStack1():
def __init__(self):
self.__stack1 = []
self.__stack2 = []
def push(self, val):
self.__stack1.append(val)
def pop_(self):
return self.__stack1.pop(-1)
def get_min(self):
"""
栈中的元素各个要出入两次,总共4次,时间复杂度为O(n)
"""
min_val = 0
while self.__stack1:
val = self.__stack1.pop(-1)
if val < min_val:
min_val = val
self.__stack2.append(val)
while self.__stack2:
self.__stack1.append(self.__stack2.pop(-1))
return min_val
# ms = MinStack1()
# for ele in [3, 4, 2, 0, -4, 99]:
# ms.push(ele)
# print(ms.pop_())
# print(ms.get_min())
class MinStack2():
def __init__(self):
self.__stack1 = []
self.__stack2 = []
def push(self, val):
"""时间复杂度O(1)"""
self.__stack1.append(val)
if not self.__stack2:
self.__stack2.append(val)
elif val < self.__stack2[-1]:
self.__stack2.append(val)
def pop_(self):
"""空间复杂度O(1)"""
if self.__stack1:
tmp = self.__stack1.pop(-1)
if tmp == self.__stack2[-1]:
self.__stack2.pop(-1)
return tmp
else:
return None
def get_min(self):
"""时间复杂度O(1)"""
if self.__stack2:
return self.__stack2[-1]
ms = MinStack2()
for ele in [3, 4, 2, 0, -4, 99]:
ms.push(ele)
print(ms.pop_())
print(ms.get_min())
例5: 最大直方图
给出一个直方图,求最大矩形面积(leetcode84)
- 用堆栈计算每一块板能够神道的左右边界
- 对每一块板
- 这一块左边界确定,入栈
- 堆栈顶高,堆栈顶右边界确定,出栈,计算面积
- 入栈时左边界确定
- 出栈时,右边界确定
- 堆栈里面的元素时递增的
- 本质:中间的短板没有用
- 复杂度O(n)
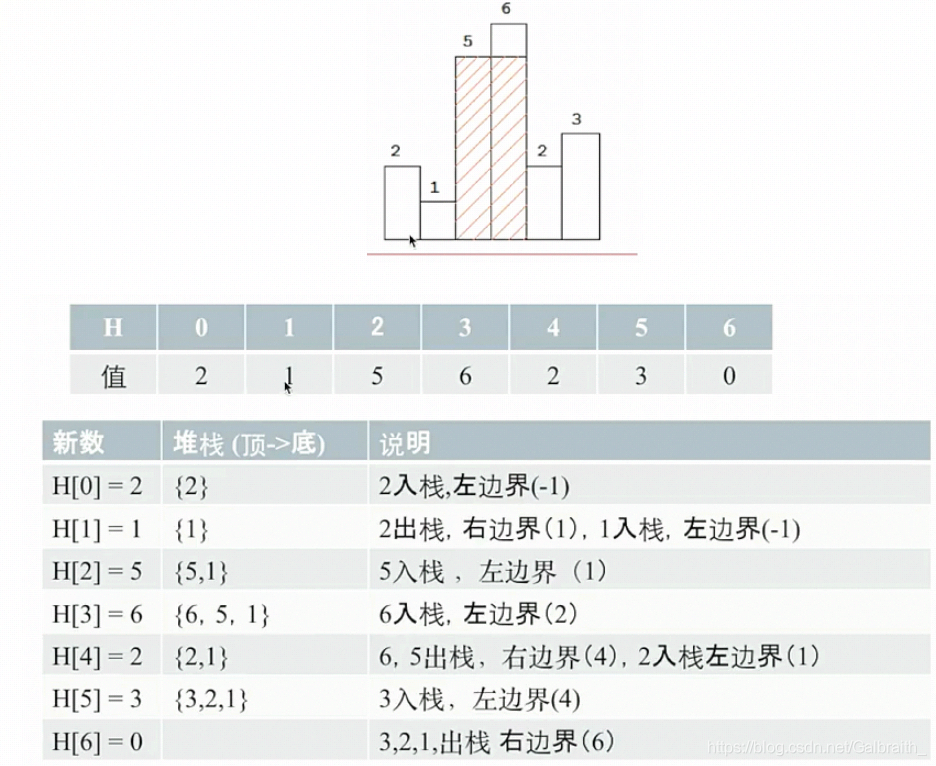
"""
初始化一个栈,用来存储矩形的高,新的矩形高比栈顶元素高,那么新矩形的左边界是确定的;
新的矩形的高比栈顶矮,栈顶元素的右边界就确定了,出栈计算面积
"""
def max_area(h):
n = len(h)
ans = 0
stack = []
for i in range(0, n):
if not stack or h[stack[-1]] < h[i]:
stack.append(i)
else:
while stack and h[stack[-1]] >= h[i]:
h_ = stack.pop(-1)
if not stack:
length = i
else:
length = i - stack[-1] - 1
ans = max(0, length * h[h_])
stack.append(i)
return ans
test = [2, 1, 5, 6, 2, 3]
max_area(test)
例6:滑动窗口最大值
给定一个数组a[0…n],还有一个最大值k,计算数组b[i] = max(a[i-k+1…i]),注意负数对应的值是无穷小
- 方法1: 用一个最大值存放最近的k个数
- 计算好b[i-1]
- a[i-k]处堆,如何找到a[i-k]
- a[i]入堆
- b[i]=堆顶
- 时间复杂度O(nlogk)
- 方法2
- 我们同时存一个旧数x,和一个新数y并且x<=y,则x永远不会我们想要的解,因为:
- “窗口”朝右滑动{for i in range(n)}
- x先离开窗口
- y进入窗口后x与y总是同时存在,直到x离开
- x没用了…利用这个性质?
- 双端队列,对头存旧的数,队尾存新的数
- 如果队尾的数<= 将要入队的数a[i],则扔掉队尾的数
- 队列里面从队头到队尾是递减的,队头永远是窗口最大值
- 考虑
- 队头何时过期?
- 时间复杂度O(n),每个元素出入队一次;
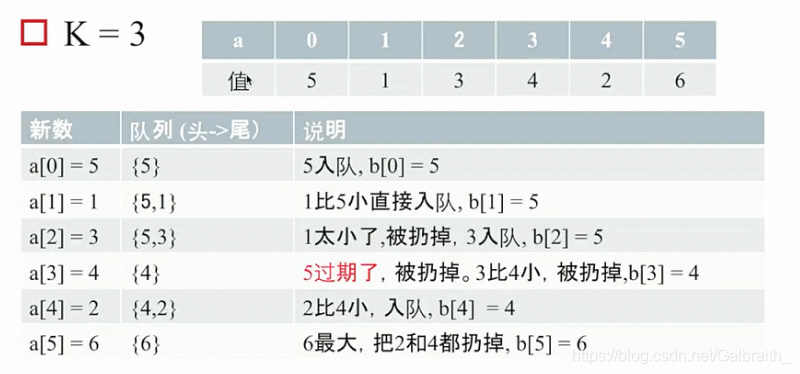
- 我们同时存一个旧数x,和一个新数y并且x<=y,则x永远不会我们想要的解,因为:
def max_k_sum(nums, k):
"""
时间复杂度为O(n)
"""
# 建立辅助双端队列,用于存放
idx_q = []
n = len(nums)
ans = [0] * n
for i in range(n):
# 查看队头的元素是否过期
# 保证三个滑动框
while idx_q and idx_q[0] <= i - k:
# 扔掉队头
idx_q.pop(0)
# 队头元素是否小于即将入队的值
while idx_q and nums[idx_q[-1]] <= nums[i]:
# 扔掉队尾
idx_q.pop(-1)
# 注意入队的是下标
idx_q.append(i)
ans[i] = nums[idx_q[0]]
return ans
print(max_k_sum([2, 1, 0, 4, 3, 9, 5, 7], 3))
- 理解:
- 旧的数比较大,因为“过期”而不得不出队
- 存放a数组的下标而没存放具体值
- 扩展
- 如果输入的是一个流,我们必须自己保存“时间戳”,决定过期
总结
- 理解队列堆栈的基本概念
- n个左右括号的出入栈顺序有多少种?
- 熟悉队列、堆栈的应用
- 递归和非递归的转化dfs
- BFS搜索
- 维护队列和堆栈的单挑性
- 利用顺序