「中高级前端」窥探数据结构的世界- ES6版

2023-01-12 21:19:30

1. 什么是数据结构？

数据结构是在计算机中组织和存储数据的一种特殊方式，使得数据可以高效地被访问和修改。更确切地说，数据结构是数据值的集合，表示数据之间的关系，也包括了作用在数据上的函数或操作。

1.1 为什么我们需要数据结构？

数据是计算机科学当中最关键的实体，而数据结构则可以将数据以某种组织形式存储，因此，数据结构的价值不言而喻。
无论你以何种方式解决何种问题，你都需要处理数据——无论是涉及员工薪水、股票价格、购物清单，还是只是简单的电话簿问题。
数据需要根据不同的场景，按照特定的格式进行存储。有很多数据结构能够满足以不同格式存储数据的需求。

1.2 八大常见的数据结构

数组： Array
堆栈： Stack
队列： Queue
链表： Linked Lists
树： Trees
图： Graphs
字典树： Trie
散列表（哈希表）： Hash Tables

在较高的层次上，基本上有三种类型的数据结构:

堆栈和队列是类似于数组的结构，仅在项目的插入和删除方式上有所不同。
链表，树，和图结构的节点是引用到其他节点。
散列表依赖于散列函数来保存和定位数据。

在复杂性方面：

堆栈和队列是最简单的，并且可以从中构建链表。
树和图是最复杂的，因为它们扩展了链表的概念。
散列表和字典树需要利用这些数据结构来可靠地执行。

就效率而已：

链表是记录和存储数据的最佳选择
而哈希表和字典树在搜索和检索数据方面效果最佳。

2.数组 - 知识补充

数组是最简单的数据结构，这里就不讲过多了。贴一张每个函数都运行10,000次迭代：

10,000个随机密钥在10,000个对象的数组中查找的执行效率对比图：

[	
  {	
    id: "key0",	
    content: "I ate pizza 0 times"	
  },	
  {	
    id: "key1",	
    content: "I ate pizza 1 times"	
  },	
  {	
    id: "key2",	
    content: "I ate pizza 2 times"	
  },	
  ...	
]	
	
["key284", "key958", "key23", "key625", "key83", "key9", ... ]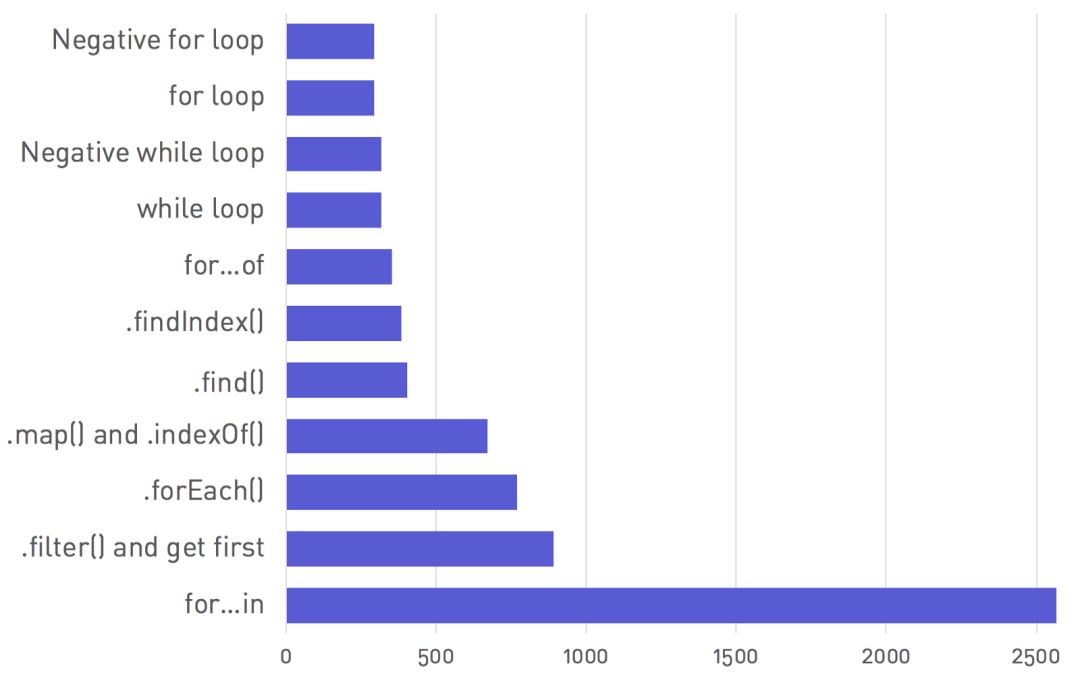

640?wx_fmt=png

2.1 `for...in`为何这么慢？

for...in语法令人难以置信的缓慢。在测试中就已经比正常情况下慢近9倍的循环。

这是因为 for...in语法是第一个能够迭代对象键的JavaScript语句。

循环对象键（ {}）与在数组（ []）上进行循环不同，

因为引擎会执行一些额外的工作来跟踪已经迭代的属性。

3. 堆栈： `Stack`

640?wx_fmt=png 堆栈是元素的集合，可以在顶部添加项目，我们有几个实际的堆栈示例：

浏览器历史记录
撤消操作
递归以及其它。

三句话解释堆栈：

两个原则操作： push和 pop。 Push 将元素添加到数组的顶部，而 Pop将它们从同一位置删除。
遵循" Last In，First Out"，即： LIFO，后进先出。
没了。

3.1 堆栈的实现。

请注意，下方例子中，我们可以颠倒堆栈的顺序：底部变为顶部，顶部变为底部。

因此，我们可以分别使用数组 unshift和 shift方法代替 push和 pop。

class Stack {	
    constructor(...items) {	
        this.reverse = false;	
        this.stack = [...items];	
    }	
	
    push(...items) {	
        return this.reverse	
            ? this.stack.unshift(...items)	
            : this.stack.push(...items);	
    }	
	
    pop() {	
        return this.reverse ? this.stack.shift() : this.stack.pop();	
    }	
}	
	
const stack = new Stack(4, 5);	
stack.reverse = true;	
console.log(stack.push(1, 2, 3) === 5) // true	
console.log(stack.stack ===[1, 2, 3, 4, 5]) // true

4. 队列： `Queue`

在计算机科学中，一个队列(queue)是一种特殊类型的抽象数据类型或集合。集合中的实体按顺序保存。

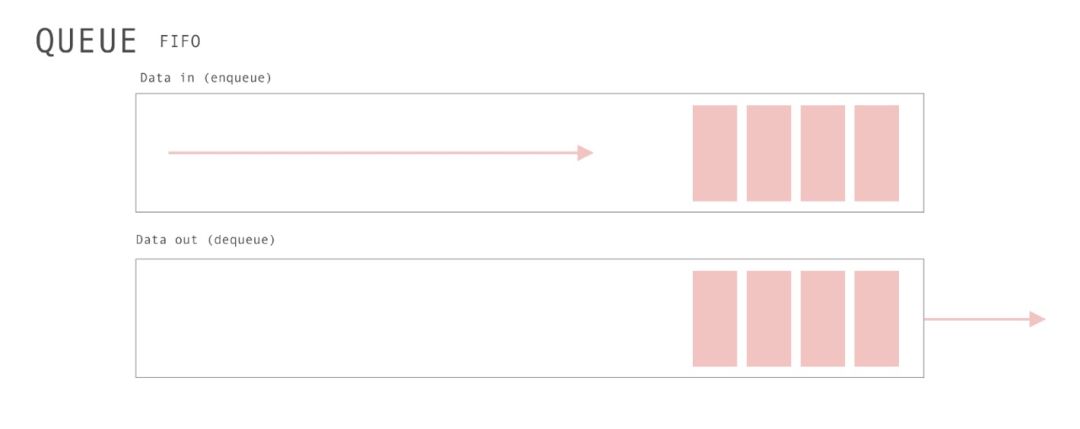640?wx_fmt=png 而在前端开发中，最著名的队列使用当属浏览器/NodeJs中关于宏任务与微任务，任务队列的知识。这里就不再赘述了。

在后端领域，用得最广泛的就是消息队列： Messagequeue：如 RabbitMQ、 ActiveMQ等。

以编程思想而言， Queue可以用两句话描述：

只是具有两个主要操作的数组： unshift和 pop。
遵循 "Fist In，first out"即： FIFO，先进先出。

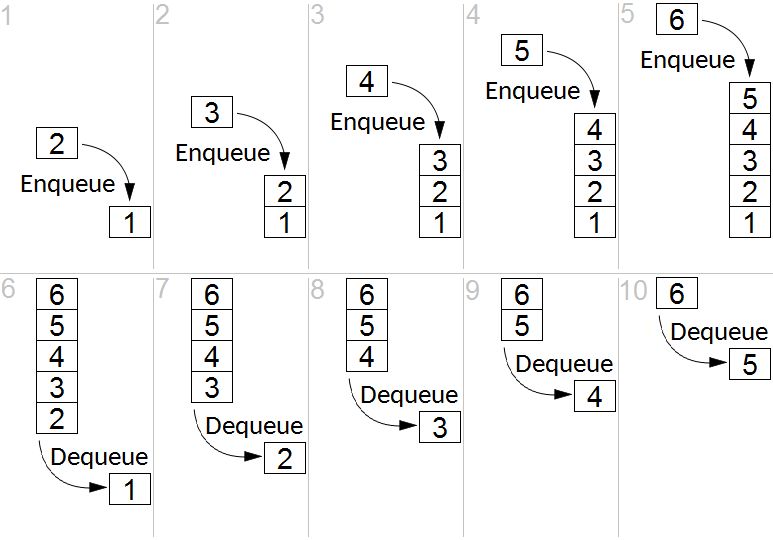
640?wx_fmt=png

4.1 队列的实现

请注意，下方例子中，我们可以颠倒堆队列的顺序。

因此，我们可以分别使用数组 unshift和 shift方法代替 push和 pop。

class Queue {	
    constructor(...items) {	
        this.reverse = false;	
        this.queue = [...items];	
    }	
	
    enqueue(...items) {	
        return this.reverse	
            ? this.queue.push(...items)	
            : this.queue.unshift(...items);	
    }	
	
    dequeue() {	
        return this.reverse ? this.queue.shift() : this.queue.pop();	
    }	
}

5. 链表： `LinkedLists`

与数组一样，链表是按顺序存储数据元素。

链表不是保留索引，而是指向其他元素。

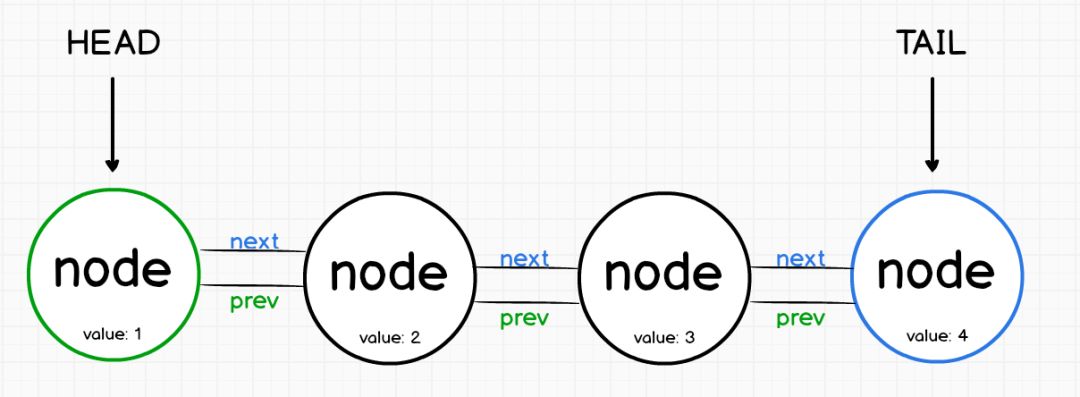640?wx_fmt=png 第一个节点称为头部( head)，而最后一个节点称为尾部( tail)。

单链表与双向链表：

单链表是表示一系列节点的数据结构，其中每个节点指向列表中的下一个节点。
链表通常需要遍历整个操作列表，因此性能较差。
提高链表性能的一种方法是在每个节点上添加指向列表中上一个节点的第二个指针。
双向链表具有指向其前后元素的节点。

链表的优点：

链接具有常量时间插入和删除，因为我们可以只更改指针。
与数组一样，链表可以作为堆栈运行。

链表的应用场景：

链接列表在客户端和服务器上都很有用。

在客户端上，像 Redux就以链表方式构建其中的逻辑。
React 核心算法 React Fiber的实现就是链表。

640?wx_fmt=png

- React Fiber之前的 Stack Reconciler，是自顶向下的递归 mount/update，无法中断(持续占用主线程)，这样主线程上的布局、动画等周期性任务以及交互响应就无法立即得到处理，影响体验。
- React Fiber解决过去 Reconciler存在的问题的思路是把渲染/更新过程(递归diff)拆分成一系列小任务，每次检查树上的一小部分，做完看是否还有时间继续下一个任务，有的话继续，没有的话把自己挂起，主线程不忙的时候再继续。
在服务器上，像 Express这样的 Web框架也以类似的方式构建其中间件逻辑。当请求被接收时，它从一个中间件管道输送到下一个，直到响应被发出。

5.1 单链表实现

单链表的操作核心有：

push（value） - 在链表的末尾/头部添加一个节点
pop（） - 从链表的末尾/头部删除一个节点
get（index） - 返回指定索引处的节点
delete（index） - 删除指定索引处的节点
isEmpty（） - 根据列表长度返回true或false
print（） - 返回链表的可见表示

class Node {	
  constructor(data) {	
    this.data = data	
    this.next = null	
  }	
}	
	
class LinkedList {	
  constructor() {	
    this.head = null	
    this.tail = null	
    // 长度非必要	
    this.length = 0	
  }	
  push(data) {	
    // 创建一个新节点	
    const node = new Node(data)	
    // 检查头部是否为空	
    if (this.head === null) {	
      this.head = node	
      this.tail = node	
    } 	
    this.tail.next = node	
    this.tail = node	
    this.length++	
  }	
  pop(){	
    // 先检查链表是否为空	
    if(this.isEmpty()) {	
      return null	
    } 	
    // 如果长度为1	
    if (this.head === this.tail) {	
      this.head = null	
      this.tail = null	
      this.length--	
      return this.tail	
    }	
    let node = this.tail	
    let currentNode = this.head	
    let penultimate	
	
    while (currentNode) {	
      if (currentNode.next === this.tail) {	
        penultimate = currentNode	
        break	
      }	
      currentNode = currentNode.next	
    }	
	
    penultimate.next = null	
    this.tail = penultimate	
    this.length --	
    return node	
  }	
	
  get(index){	
    // 处理边界条件	
    if (index === 0) {	
      return this.head	
    }	
    if (index &lt; 0 || index &gt; this.length) {	
      return null	
    }	
	
    let currentNode = this.head	
    let i = 0	
    while(i &lt; index) {	
      i++	
      currentNode = currentNode.next	
    }	
    return currentNode	
	
  }	
  delete(index){	
    let currentNode = this.head	
	
    if (index === 0) {	
      let deletedNode	
      currentNode.next = this.head	
      deletedNode = currentNode	
      this.length--	
	
      return deletedNode	
    }	
	
    if (index &lt; 0 || index &gt; this.length) {	
      return null	
    }	
	
    let i = 0	
    let previous	
	
    while(i &lt; index) {	
      i++	
      previous = currentNode	
      currentNode = currentNode.next	
    }	
    previous.next = currentNode.next	
    this.length--	
    return currentNode	
  }	
	
  isEmpty() {	
    return this.length === 0	
  }	
  print() {	
    const list = []	
    let currentNode = this.head	
    while(currentNode){	
      list.push(currentNode.data)	
      currentNode = currentNode.next	
    }	
    return list.join(' =&gt; ')	
  }	
}

测试一下：

const l = new LinkedList()	
	
// 添加节点	
const values = ['A', 'B', 'C']	
values.forEach(value =&gt; l.push(value))	
	
console.log(l)	
console.log(l.pop())	
console.log(l.get(1))	
console.log(l.isEmpty())	
console.log(l.print())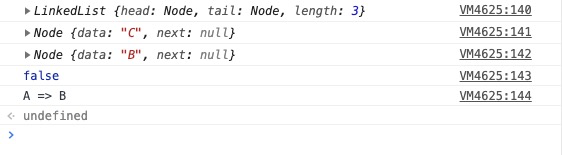

640?wx_fmt=png

5.2 双向链表实现

1. 双向链表的设计

类似于单链表，双向链表由一系列节点组成。每个节点包含一些数据以及指向列表中下一个节点的指针和指向前一个节点的指针。这是 JavaScript中的简单表示：

class Node {	
    constructor(data) {	
        // data 包含链表项应存储的值	
        this.data = data;	
        // next 是指向列表中下一项的指针	
        this.next = null;	
        // prev 是指向列表中上一项的指针	
        this.prev = null;	
    }	
}

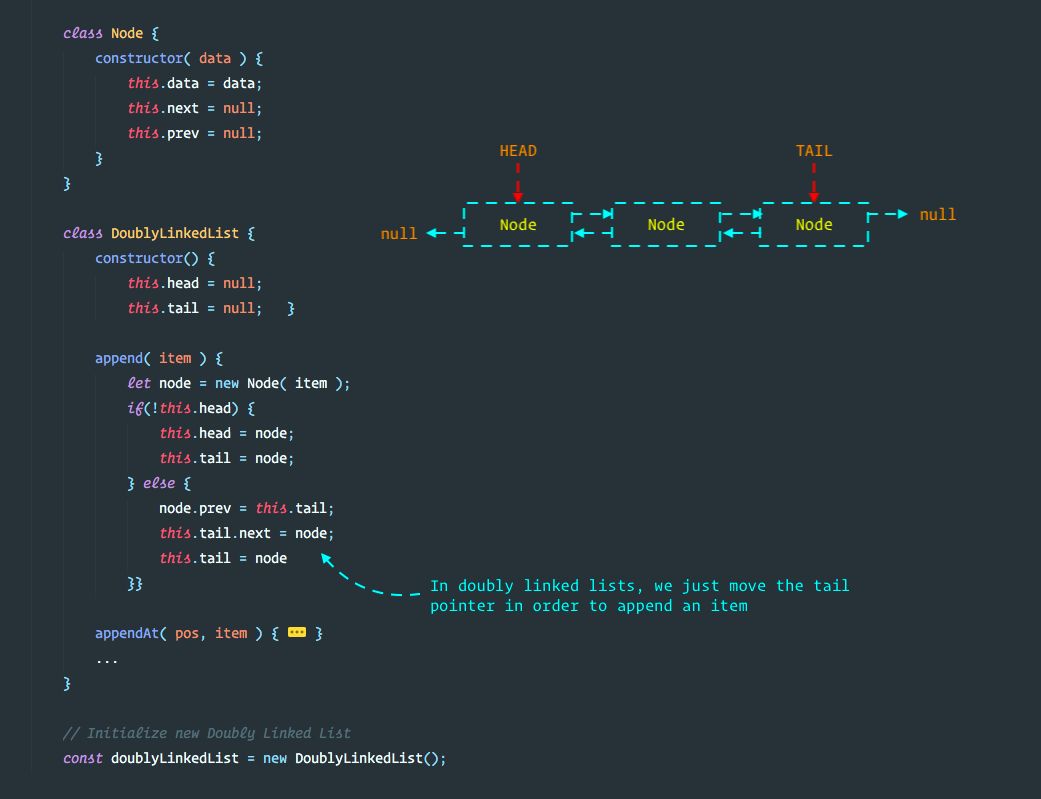640?wx_fmt=png 还是敲一遍吧：

class DoublyLinkedList {	
    constructor() {	
        this.head = null;	
        this.tail = null;	
    }	
    // 各种操作方法	
    // ...	
}

2. 双向链表的操作方法

640?wx_fmt=png

Append & AppendAt: 在链表的尾部/ 指定位置添加节点

append( item ) {	
  let node = new Node( item );	
  if(!this.head) {	
    this.head = node;	
    this.tail = node;	
  } else {	
    node.prev = this.tail;	
    this.tail.next = node;	
    this.tail = node	
  }	
}

640?wx_fmt=png

appendAt( pos, item ) {	
   let current = this.head;	
   let counter = 1;	
   let node = new Node( item );	
   if( pos == 0 ) {	
     this.head.prev = node	
     node.next = this.head	
     this.head = node	
   } else {	
     while(current) {	
      current = current.next;	
      if( counter == pos ) {	
        node.prev = current.prev	
        current.prev.next = node	
        node.next = current	
        current.prev = node	
      }	
      counter++	
    }	
  }	
}

640?wx_fmt=png

Remove & RemoveAt: 在链表的尾部/ 指定位置删除节点

remove( item ) {	
  let current = this.head;	
  while( current ) {	
    if( current.data === item ) {	
      if( current == this.head &amp;&amp; current == this.tail ) {	
        this.head = null;	
        this.tail = null;	
      } else if ( current == this.head ) {	
        this.head = this.head.next	
        this.head.prev = null	
      } else if ( current == this.tail ) {	
        this.tail = this.tail.prev;	
        this.tail.next = null;	
      } else {	
        current.prev.next = current.next;	
        current.next.prev = current.prev;	
      }	
   }	
   current = current.next	
  }	
}

640?wx_fmt=png

removeAt( pos ) {	
  let current = this.head;	
  let counter = 1;	
  if( pos == 0 ) {	
   this.head = this.head.next;	
   this.head.prev = null;	
  } else {	
   while( current ) {	
    current = current.next	
    if ( current == this.tail ) {	
     this.tail = this.tail.prev;	
     this.tail.next = null;	
    } else if( counter == pos ) {	
     current.prev.next = current.next;	
     current.next.prev = current.prev;	
     break;	
    }	
    counter++;	
   }	
  }	
}

640?wx_fmt=png

Reverse: 翻转双向链表

reverse(){	
  let current = this.head;	
  let prev = null;	
  while( current ){	
   let next = current.next	
   current.next = prev	
   current.prev = next	
   prev = current	
   current = next	
  }	
  this.tail = this.head	
  this.head = prev	
}

640?wx_fmt=png

Swap：两节点间交换。

swap( nodeOne, nodeTwo ) {	
   let current = this.head;	
   let counter = 0;	
   let firstNode;	
   while( current !== null ) {	
     if( counter == nodeOne ){	
       firstNode = current;	
     } else if( counter == nodeTwo ) {	
       let temp = current.data;	
       current.data = firstNode.data;	
       firstNode.data = temp;	
     }	
     current = current.next;	
     counter++;	
   }	
   return true	
}

640?wx_fmt=png

IsEmpty & Length：查询是否为空或长度。

length() {	
  let current = this.head;	
  let counter = 0;	
  while( current !== null ) {	
   counter++	
   current = current.next	
  }	
  return counter;	
}	
isEmpty() {	
  return this.length() &lt; 1	
}

640?wx_fmt=png

Traverse: 遍历链表

traverse( fn ) {	
   let current = this.head;	
   while( current !== null ) {	
    fn(current)	
    current = current.next;	
   }	
   return true;	
}

640?wx_fmt=png

每一项都加10

Search：查找节点的索引。

search( item ) {	
  let current = this.head;	
  let counter = 0;	
  while( current ) {	
    if( current.data == item ) {	
     return counter	
    }	
    current = current.next	
    counter++	
  }	
  return false;	
}

640?wx_fmt=png

6. 树： `Tree`

计算机中经常用到的一种非线性的数据结构——树（Tree），由于其存储的所有元素之间具有明显的层次特性，因此常被用来存储具有层级关系的数据，比如文件系统中的文件；也会被用来存储有序列表等。

在树结构中，每一个结点只有一个父结点，若一个结点无父节点，则称为树的根结点，简称树的根（root）。
每一个结点可以有多个子结点。
没有子结点的结点称为叶子结点。
一个结点所拥有的子结点的个数称为该结点的度。
所有结点中最大的度称为树的度。树的最大层次称为树的深度。

6.1 树的分类

常见的树分类如下，其中我们掌握二叉搜索树即可。

二叉树： Binary Search Tree
AVL树： AVL Tree
红黑树： Red-Black Tree
线段树： Segment Tree - with min/max/sum range queries examples
芬威克树： Fenwick Tree ( Binary Indexed Tree)

6.2 树的应用

DOM树。每个网页都有一个树数据结构。

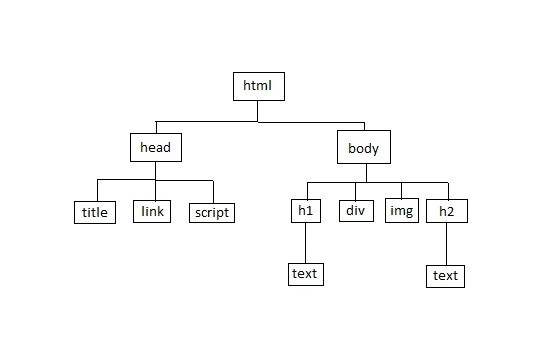
640?wx_fmt=png

Vue和 React的 Virtual DOM也是树。

6.3 二叉树： `BinarySearchTree`

二叉树是一种特殊的树，它的子节点个数不超过两个。
且分别称为该结点的左子树（left subtree）与右子树（right subtree）。
二叉树常被用作二叉查找树和二叉搜索树、或是二叉排序树（BST）。

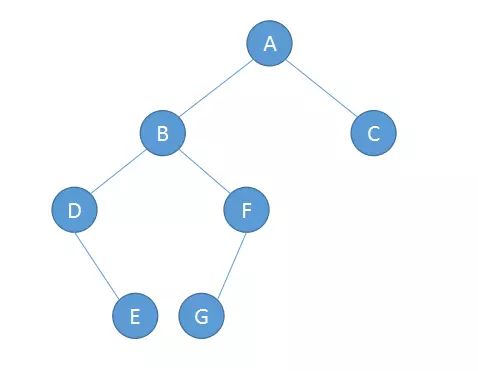
640?wx_fmt=png

6.4 二叉树的遍历

按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次，这个操作被称为树的遍历，是对树的一种最基本的运算。

由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。

按照根节点访问的顺序不同，二叉树的遍历分为以下三种：前序遍历，中序遍历，后序遍历；

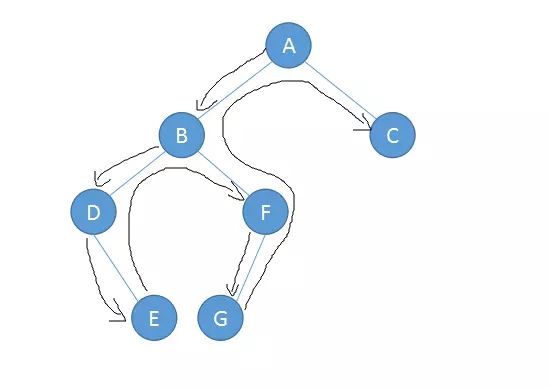
前序遍历： Pre-Order

根节点->左子树->右子树

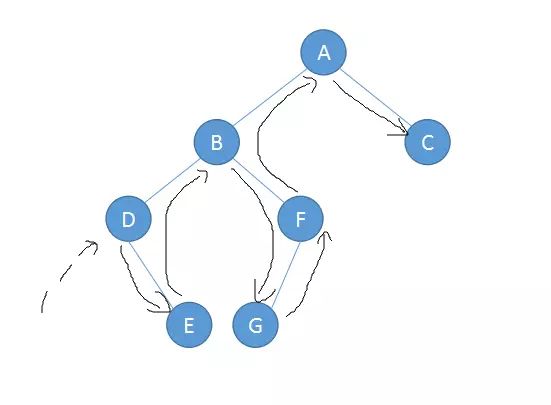
640?wx_fmt=png

中序遍历： In-Order

左子树->根节点->右子树

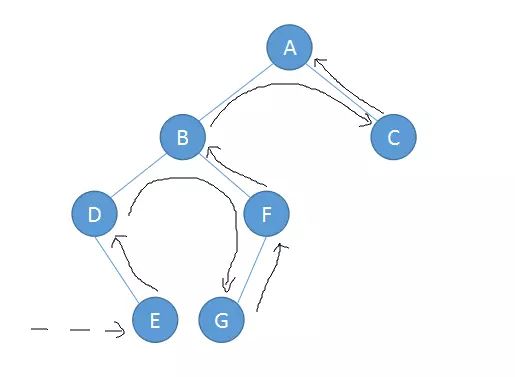
640?wx_fmt=png

后序遍历： Post-Order

左子树->右子树->根节点

640?wx_fmt=png

因此我们可以得之上面二叉树的遍历结果如下：

前序遍历：ABDEFGC
中序遍历：DEBGFAC
后序遍历：EDGFBCA

6.5 二叉树的实现

class Node { 	
  constructor(data) { 	
    this.left = null	
    this.right = null	
    this.value = value	
  } 	
} 	
	
class BST {	
    constructor() {	
        this.root = null	
    }	
    // 二叉树的各种操作	
    // insert(value) {...}	
    // insertNode(root, newNode) {...}	
    // ...

1. `insertNode`& `insert`：插入新子节点/节点

  insertNode(root, newNode) {	
    if (newNode.value &lt; root.value) {	
      // 先执行无左节点操作	
      (!root.left) ? root.left = newNode : this.insertNode(root.left, newNode)	
    } else {	
      (!root.right) ? root.right = newNode : this.insertNode(root.right, newNode)	
    }	
  }	
	
insert(value) {	
    let newNode = new Node(value)	
    // 如果没有根节点	
    if (!this.root) {	
      this.root = newNode	
    } else {	
      this.insertNode(this.root, newNode)	
    }	
}

2. `removeNode`& `remove`：移除子节点/节点

  removeNode(root, value) {	
    if (!root) {	
      return null	
    }	
	
    // 从该值小于根节点开始判断	
    if (value &lt; root.value) {	
      root.left = this.removeNode(root.left, value)	
      return root	
    } else if (value &gt; root.value) {	
      root.right = tis.removeNode(root.right, value)	
      return root	
    } else {	
      // 如果没有左右节点	
      if (!root.left &amp;&amp; !root.right) {	
        root = null	
        return root	
      }	
	
      // 存在左节点	
      if (root.left) {	
        root = root.left	
        return root	
      // 存在右节点	
      } else if (root.right) {	
        root = root.right	
        return root	
      }	
	
      // 获取正确子节点的最小值以确保我们有有效的替换	
      let minRight = this.findMinNode(root.right)	
      root.value = minRight.value	
      // 确保删除已替换的节点	
      root.right = this.removeNode(root.right, minRight.value)	
      return root	
    }	
  }	
	
remove(value) {	
    if (!this.root) {	
      return 'Tree is empty!'	
    } else {	
      this.removeNode(this.root, value)	
    }	
}

3. `findMinNode`:获取子节点的最小值

findMinNode(root) {	
    if (!root.left) {	
      return root	
    } else {	
      return this.findMinNode(root.left)	
    }	
}

4. `searchNode` & `search`：查找子节点/节点

searchNode(root, value) {	
    if (!root) {	
      return null	
    }	
	
    if (value &lt; root.value) {	
      return this.searchNode(root.left, value)	
    } else if (value &gt; root.value) {	
      return this.searchNode(root.right, value)	
    }	
	
    return root	
}	
	
search(value) {	
    if (!this.root) {	
      return 'Tree is empty'	
    } else {	
      return Boolean(this.searchNode(this.root, value))	
    }	
}

Pre-Order：前序遍历

preOrder(root) {	
    if (!root) {	
      return 'Tree is empty'	
    } else {	
      console.log(root.value)	
      this.preOrder(root.left)	
      this.preOrder(root.right)	
    }	
  }

In-Order：中序遍历

inOrder(root) {	
    if (!root) {	
      return 'Tree is empty'	
    } else {	
      this.inOrder(root.left)	
      console.log(root.value)	
      this.inOrder(root.right)	
    }	
  }

Post-Order：后序遍历

postOrder(root) {	
    if (!root) {	
      return 'Tree is empty'	
    } else {	
      this.postOrder(root.left)	
      this.postOrder(root.right)	
      console.log(root.value)	
    }	
}

7. 图： `Graph`

图是由具有边的节点集合组成的数据结构。图可以是定向的或不定向的。

图的介绍普及，找了一圈文章，还是这篇最佳：

Graphs—-A Visual Introduction for Beginners

640?wx_fmt=jpeg

7.1 图的应用

在以下场景中，你都使用到了图：

使用搜索服务，如 Google，百度。
使用 LBS地图服务，如高德，谷歌地图。
使用社交媒体网站，如微博， Facebook。

640?wx_fmt=png

图用于不同的行业和领域：

GPS系统和谷歌地图使用图表来查找从一个目的地到另一个目的地的最短路径。
社交网络使用图表来表示用户之间的连接。
Google搜索算法使用图来确定搜索结果的相关性。
运营研究是一个使用图来寻找降低运输和交付货物和服务成本的最佳途径的领域。
甚至化学使用图来表示分子！

图，可以说是应用最广泛的数据结构之一，真实场景中处处有图。

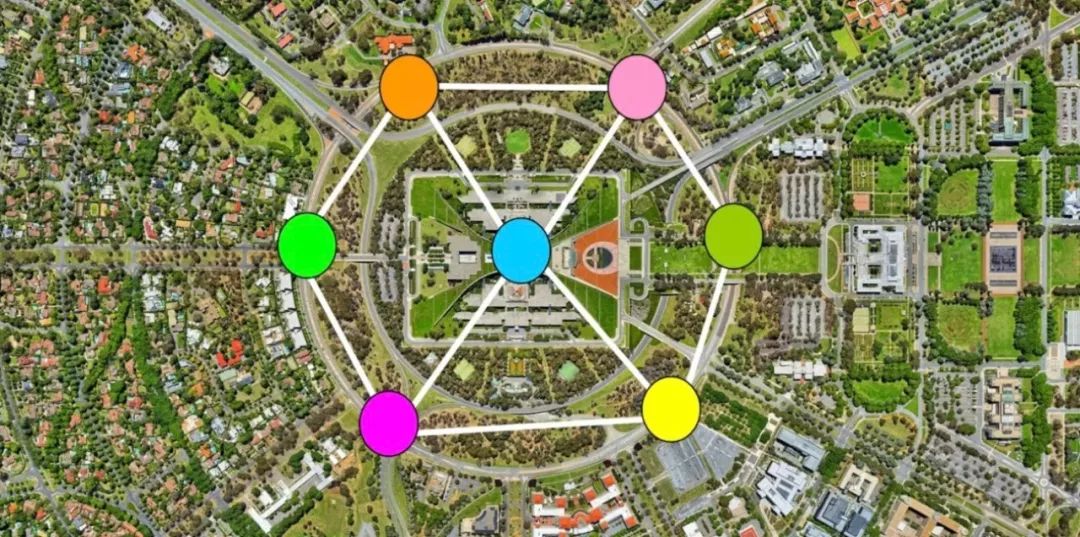
7.2 图的构成

图表用于表示，查找，分析和优化元素（房屋，机场，位置，用户，文章等）之间的连接。

640?wx_fmt=png

1. 图的基本元素

节点： Node，比如地铁站中某个站/多个村庄中的某个村庄/互联网中的某台主机/人际关系中的人.
边： Edge，比如地铁站中两个站点之间的直接连线, 就是一个边。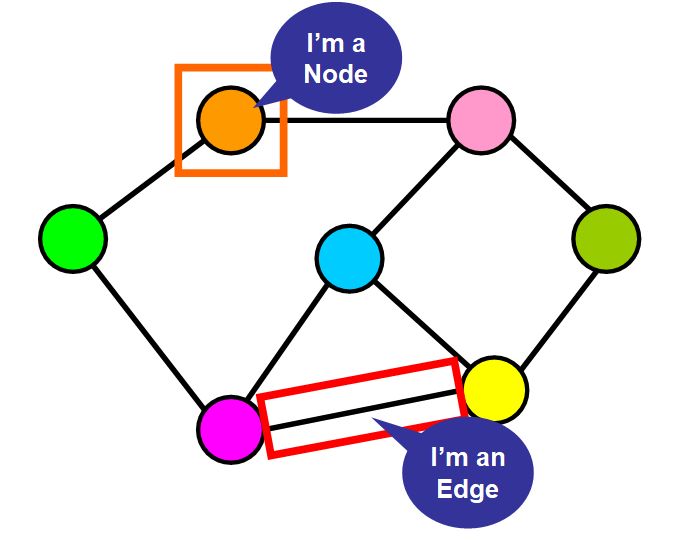

2. 符号和术语

|V|=图中顶点（节点）的总数。
|E|=图中的连接总数（边）。

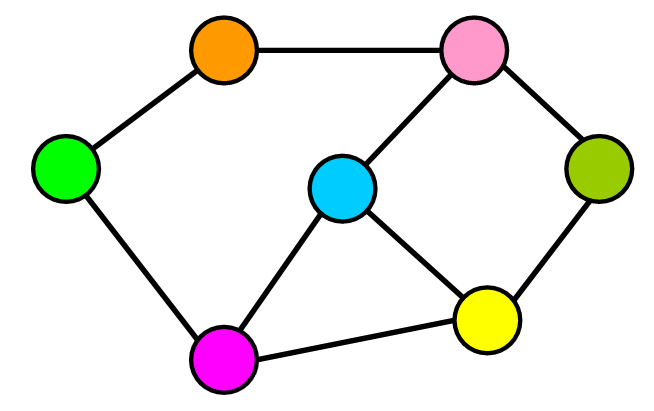
在下面的示例中

|V| = 6 	
|E| = 7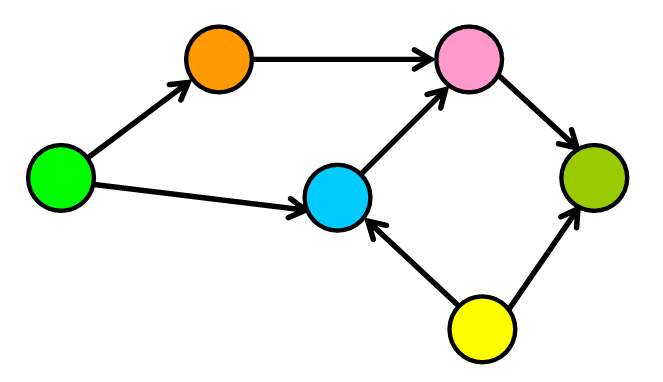

640?wx_fmt=png

3. 有向图与无向图

图根据其边（连接）的特征进行分类。

1. 有向图

在有向图中，边具有方向。它们从一个节点转到另一个节点，并且无法通过该边返回到初始节点。

如下图所示，边（连接）现在具有指向特定方向的箭头。将这些边视为单行道。您可以向一个方向前进并到达目的地，但是你无法通过同一条街道返回，因此您需要找到另一条路径。

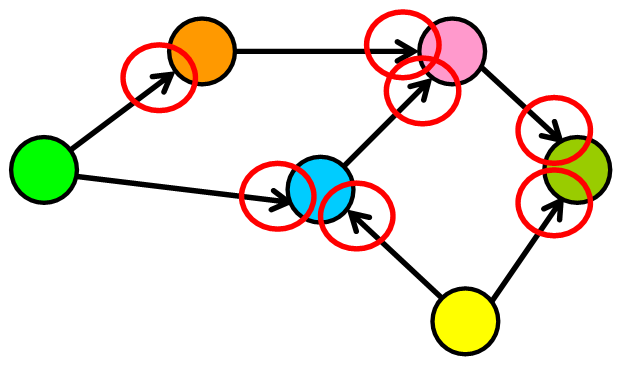
640?wx_fmt=png

有向图

2. 无向图

在这种类型的图中，边是无向的（它们没有特定的方向）。将无向边视为双向街道。您可以从一个节点转到另一个节点并返回相同的“路径”。

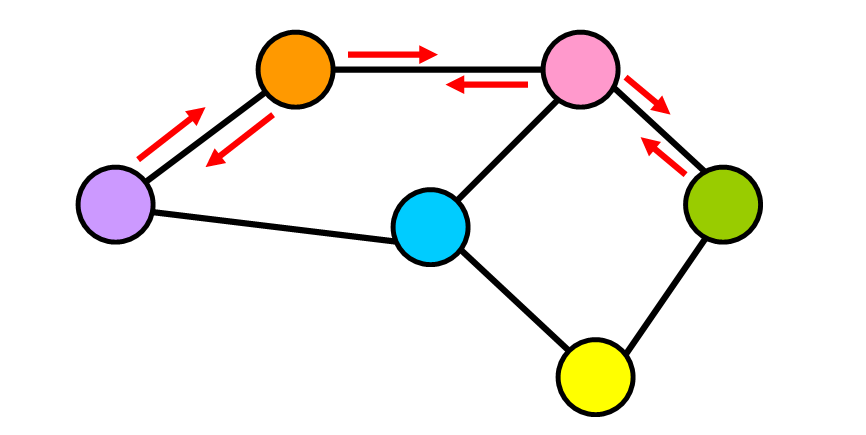
640?wx_fmt=png

4. 加权图

在加权图中，每条边都有一个与之相关的值（称为权重）。该值用于表示它们连接的节点之间的某种可量化关系。例如：

权重可以表示距离，时间，社交网络中两个用户之间共享的连接数。
或者可以用于描述您正在使用的上下文中的节点之间的连接的任何内容。

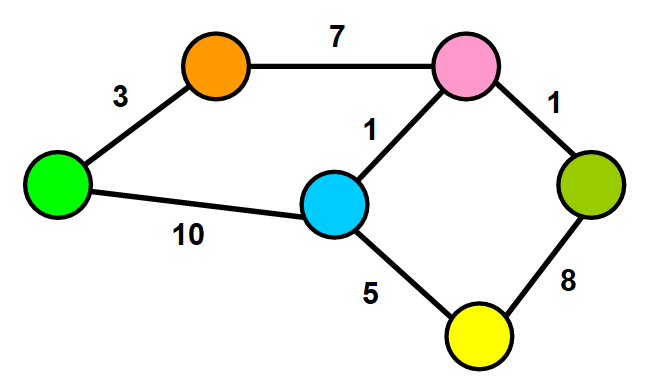
640?wx_fmt=png

著名的 Dijkstra算法，就是使用这些权重通过查找网络中节点之间的最短或最优的路径来优化路由。

5. 稀疏图与密集图

当图中的边数接近最大边数时，图是密集的。

640?wx_fmt=png

密集图

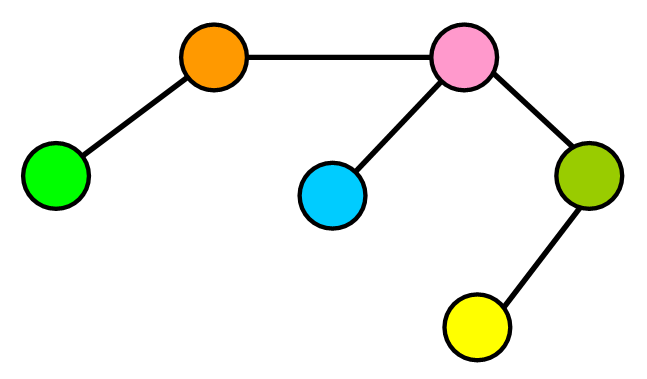
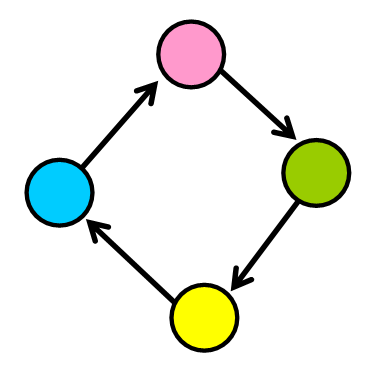
当图中的边数明显少于最大边数时，图是稀疏的。 640?wx_fmt=png

稀疏图

6. 循环

如果你按照图中的一系列连接，可能会找到一条路径，将你带回到同一节点。这就像“走在圈子里”，就像你在城市周围开车一样，你走的路可以带你回到你的初始位置。?

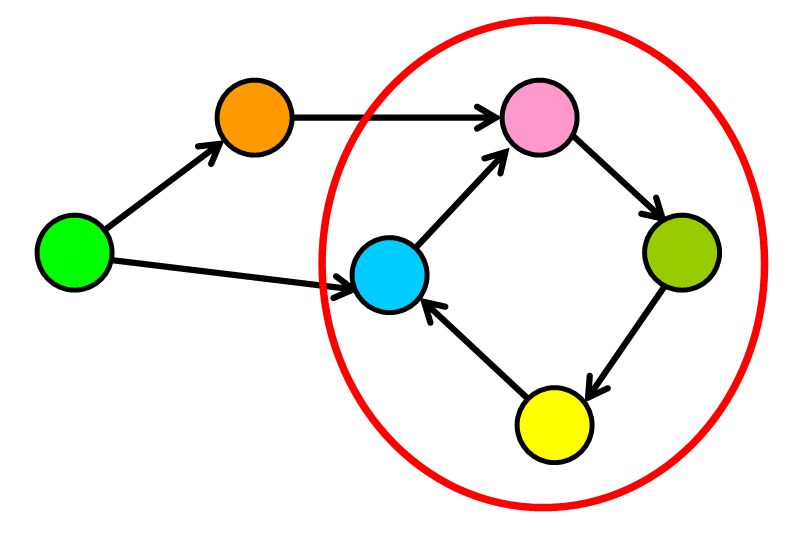
在图中，这些“圆形”路径称为“循环”。它们是在同一节点上开始和结束的有效路径。例如，在下图中，您可以看到，如果从任何节点开始，您可以通过跟随边缘返回到同一节点。

640?wx_fmt=png

循环并不总是“孤立的”，因为它们可以是较大图的一部分。可以通过在特定节点上开始搜索并找到将你带回同一节点的路径来检测它们。

640?wx_fmt=png

循环图

7.3 图的实现

我们将实现具有邻接列表的有向图。

class Graph {	
  constructor() {	
    this.AdjList = new Map();	
  }	
	
  // 基础操作方法	
  // addVertex(vertex) {}	
  // addEdge(vertex, node) {}	
  // print() {}	
}

1. `addVertex`：添加顶点

addVertex(vertex) {	
  if (!this.AdjList.has(vertex)) {	
    this.AdjList.set(vertex, []);	
  } else {	
    throw 'Already Exist!!!';	
  }	
}

尝试创建顶点：

let graph = new Graph();	
graph.addVertex('A');	
graph.addVertex('B');	
graph.addVertex('C');	
graph.addVertex('D');

打印后将会发现：

Map {	
  'A' =&gt; [],	
  'B' =&gt; [],	
  'C' =&gt; [],	
  'D' =&gt; []	
}

之所以都为空数组 '[]'，是因为数组中需要储存边( Edge)的关系。例如下图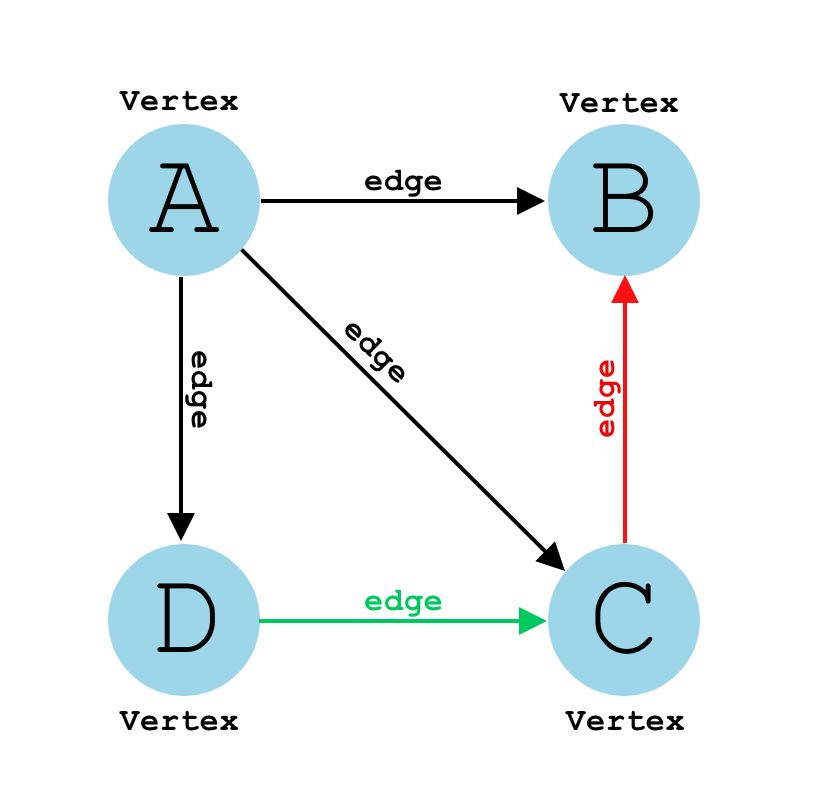： 640?wx_fmt=png 该图的 Map将为：

Map {	
  'A' =&gt; ['B', 'C', 'D'],	
  // B没有任何指向	
  'B' =&gt; [],	
  'C' =&gt; ['B'],	
  'D' =&gt; ['C']	
}

2. `addEdge`：添加边( `Edge`)

 addEdge(vertex, node) {	
    // 向顶点添加边之前，必须验证该顶点是否存在。	
    if (this.AdjList.has(vertex)) {	
      // 确保添加的边尚不存在。	
      if (this.AdjList.has(node)){	
        let arr = this.AdjList.get(vertex);	
        // 如果都通过，那么可以将边添加到顶点。	
        if(!arr.includes(node)){	
          arr.push(node);	
        }	
      }else {	
        throw `Can't add non-existing vertex -&gt;'${node}'`;	
      }	
    } else {	
      throw `You should add '${vertex}' first`;	
    }	
}

3. `print`：打印图( `Graph`)

print() {	
  for (let [key, value] of this.AdjList) {	
    console.log(key, value);	
  }	
}

测试一下

let g = new Graph();	
let arr = ['A', 'B', 'C', 'D', 'E', 'F'];	
for (let i = 0; i &lt; arr.length; i++) {	
  g.addVertex(arr[i]);	
}	
g.addEdge('A', 'B');	
g.addEdge('A', 'D');	
g.addEdge('A', 'E');	
g.addEdge('B', 'C');	
g.addEdge('D', 'E');	
g.addEdge('E', 'F');	
g.addEdge('E', 'C');	
g.addEdge('C', 'F');	
g.print();	
/* PRINTED */	
// A [ 'B', 'D', 'E' ]	
// B [ 'C' ]	
// C [ 'F' ]	
// D [ 'E' ]	
// E [ 'F', 'C' ]	
// F []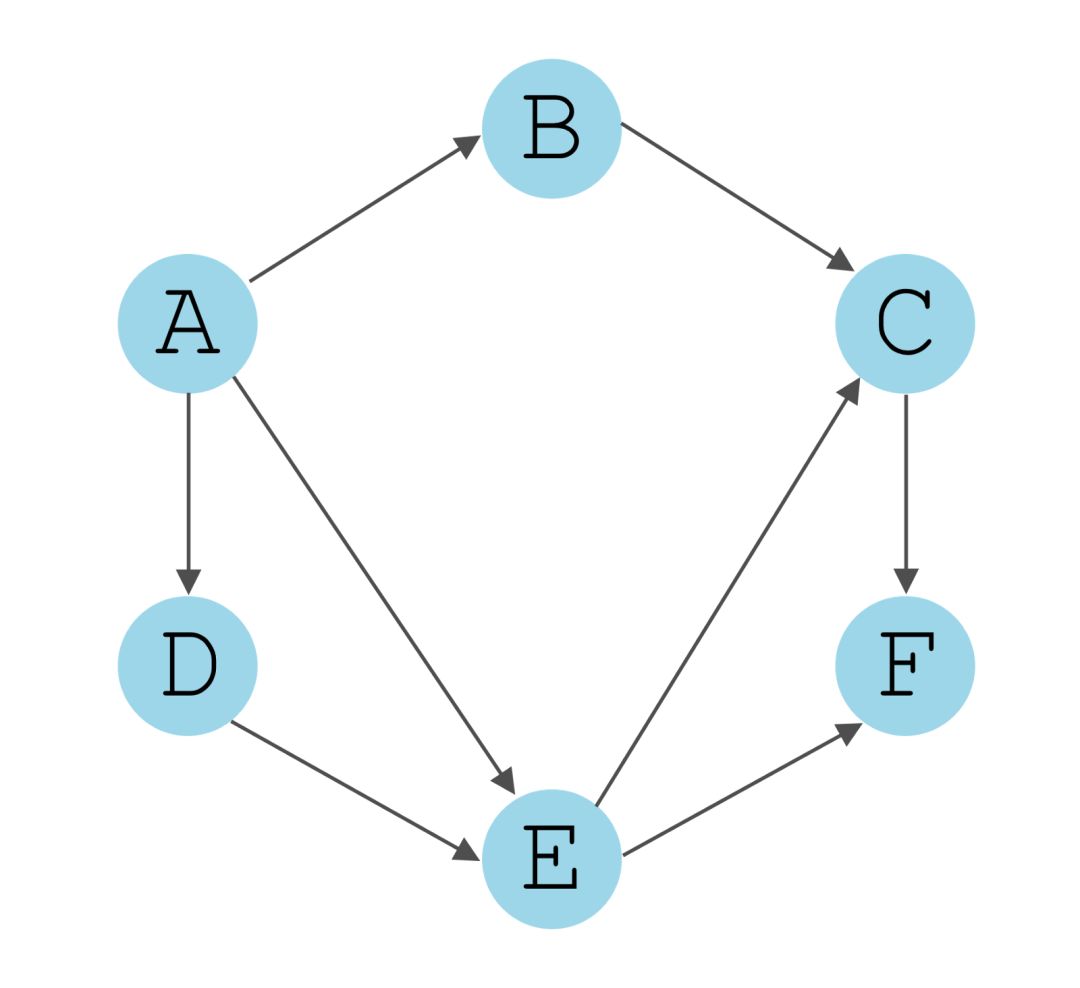

640?wx_fmt=png

到目前为止，这就是创建图所需的。但是，99％的情况下，会要求你实现另外两种方法：

广度优先算法， BFS。
深度优先算法， DFS
BFS 的重点在于队列，而 DFS 的重点在于递归。这是它们的本质区别。

5. 广度优先算法实现

广度优先算法（Breadth-First Search），同广度优先搜索。

是一种利用队列实现的搜索算法。简单来说，其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。

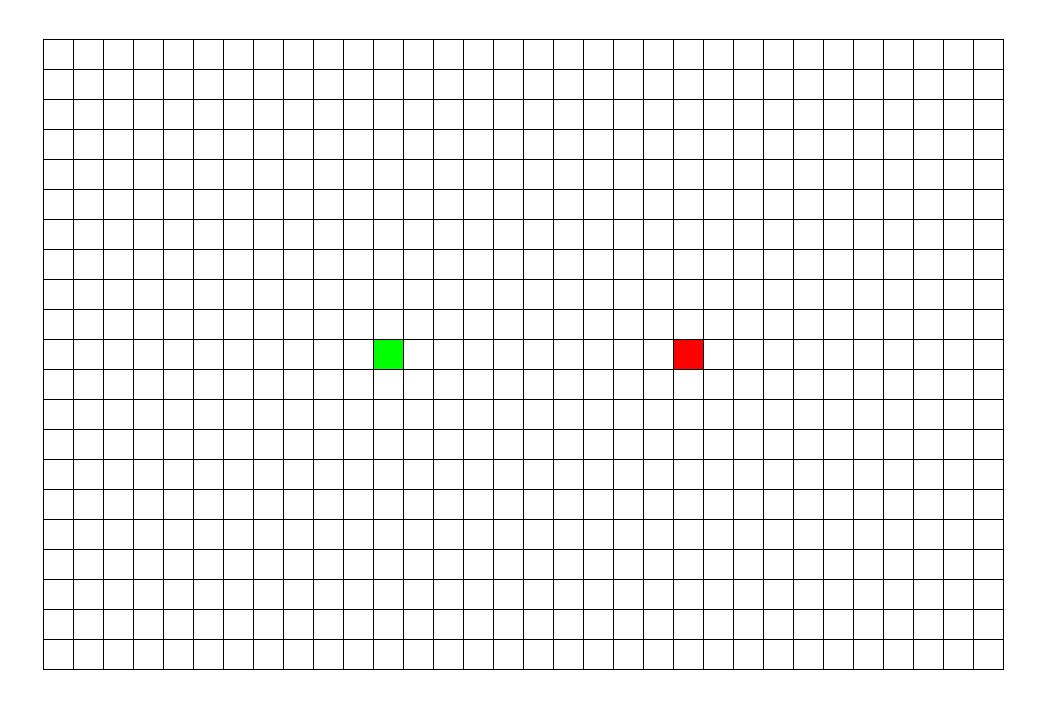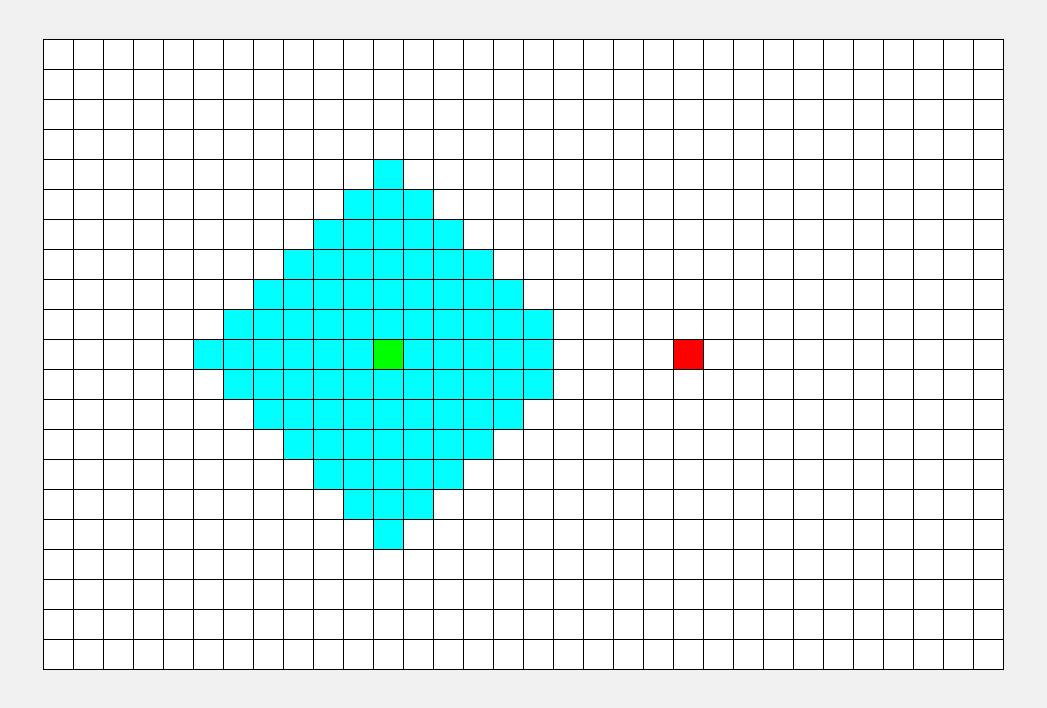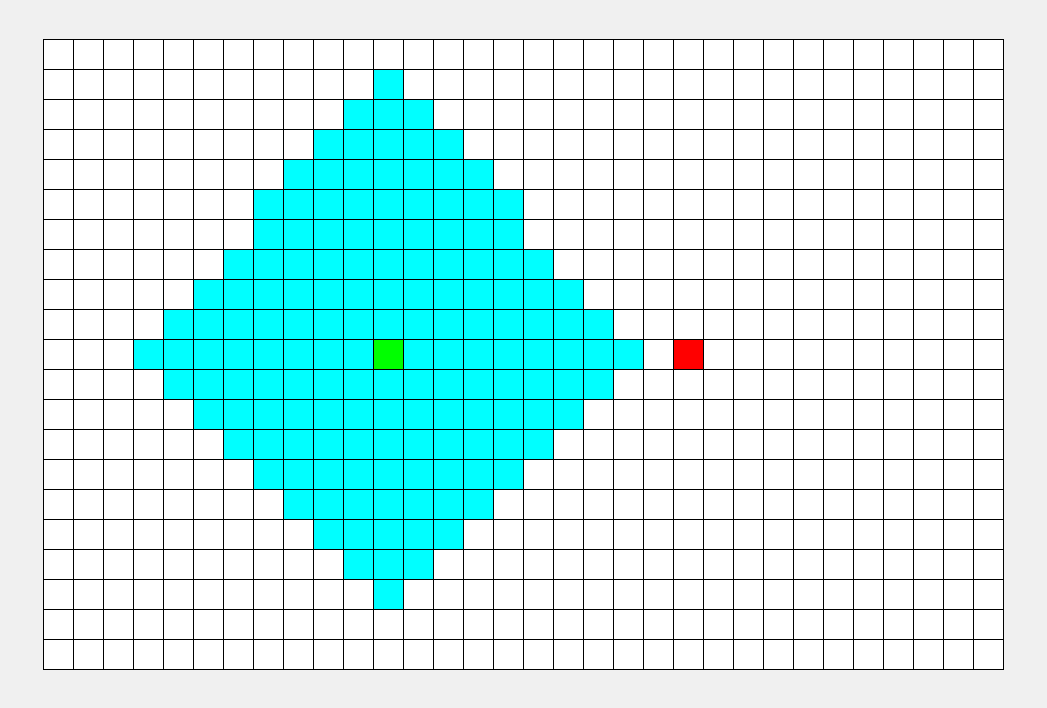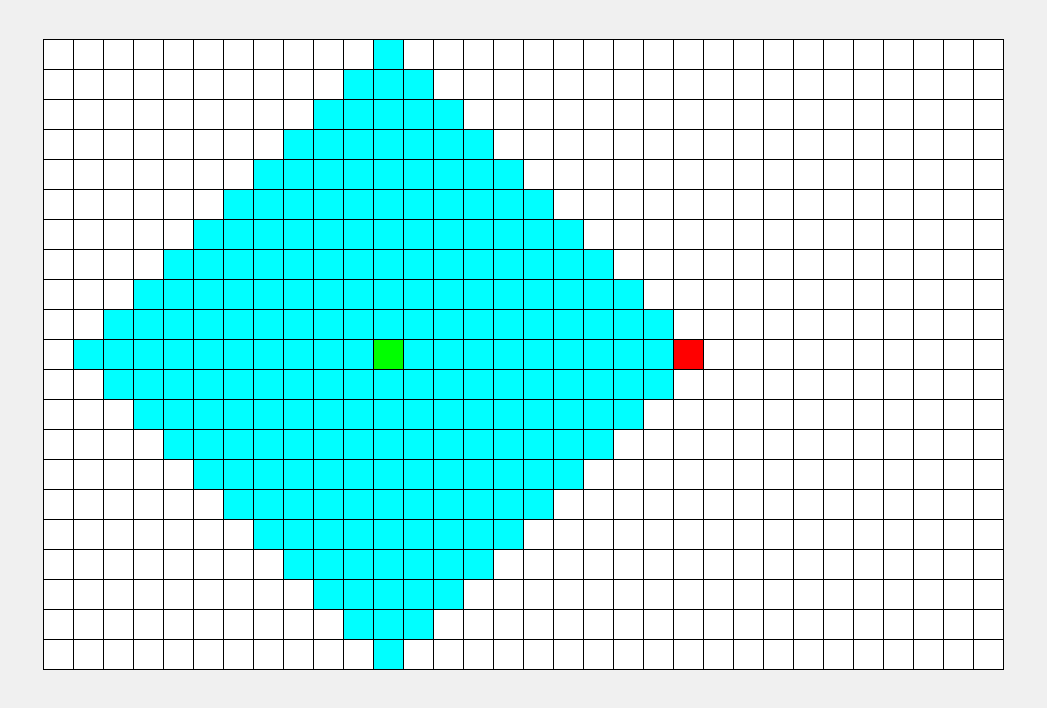640?wx_fmt=gif 如上图所示，从起点出发，对于每次出队列的点，都要遍历其四周的点。所以说 BFS 的搜索过程和 “湖面丢进一块石头激起层层涟漪” 很相似，此即 “广度优先搜索算法” 中“广度”的由来。

该算法的具体步骤为：

BFS将起始节点作为参数。（例如 'A'）
初始化一个空对象： visited。
初始化一个空数组： q，该数组将用作队列。
将起始节点标记为已访问。 （visited = {'A': true}）
将起始节点放入队列中。 （q = ['A']）
循环直到队列为空

循环内部：

从中获取元素 q并将其存储在变量中。 （let current = q.pop()）
打印当前 current
从图中获取 current的边。 （let arr = this.AdjList.get(current)）。
如果未访问元素，则将每个元素标记为已访问并将其放入队列中。

visited = {	
  'A': true,	
  'B': true,	
  'D': true,	
  'E': true	
}	
q = ['B', 'D', 'E']

具体实现：

createVisitedObject(){	
  let arr = {};	
  for(let key of this.AdjList.keys()){	
    arr[key] = false;	
  }	
  return arr;	
}	
	
bfs(startingNode){	
  let visited = this.createVisitedObject();	
  let q = [];	
	
  visited[startingNode] = true;	
  q.push(startingNode);	
	
  while(q.length){	
    let current = q.pop()	
    console.log(current);	
	
    let arr = this.AdjList.get(current);	
	
    for(let elem of arr){	
      if(!visited[elem]){	
        visited[elem] = true;	
        q.unshift(elem)	
      }	
    }	
	
  }	
}

6. 深度优先算法实现

深度优先搜索算法（Depth-First-Search，缩写为 DFS），是一种利用递归实现的搜索算法。简单来说，其搜索过程和 “不撞南墙不回头” 类似。

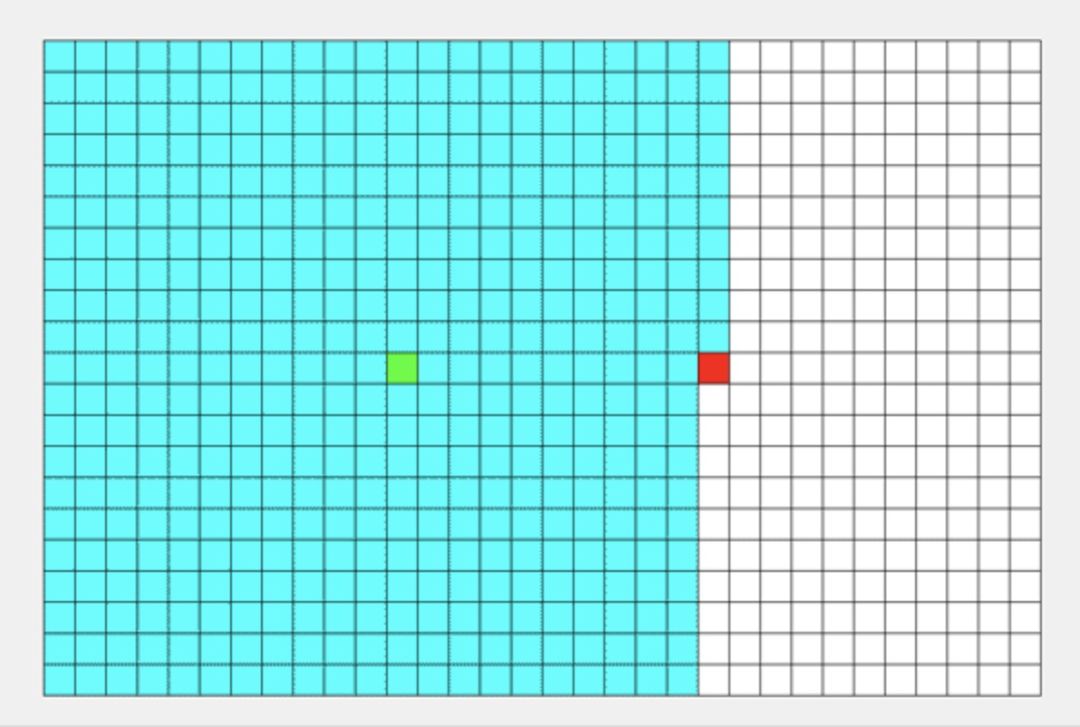
640?wx_fmt=png

如上图所示，从起点出发，先把一个方向的点都遍历完才会改变方向...... 所以说，DFS 的搜索过程和 “不撞南墙不回头” 很相似，此即 “深度优先搜索算法” 中“深度”的由来。

该算法的前期步骤和BFS相似，接受起始节点并跟踪受访节点，最后执行递归的辅助函数。

具体步骤：

接受起点作为参数 dfs(startingNode) 。
创建访问对象 let visited = this.createVisitedObject()。
调用辅助函数递归起始节点和访问对象 this.dfsHelper(startingNode, visited)。
dfsHelper 将其标记为已访问并打印出来。

createVisitedObject(){	
  let arr = {};	
  for(let key of this.AdjList.keys()){	
    arr[key] = false;	
  }	
  return arr;	
}	
	
 dfs(startingNode){	
    console.log('\nDFS')	
    let visited = this.createVisitedObject();	
    this.dfsHelper(startingNode, visited);	
  }	
	
  dfsHelper(startingNode, visited){	
    visited[startingNode] = true;	
    console.log(startingNode);	
	
    let arr = this.AdjList.get(startingNode);	
	
    for(let elem of arr){	
      if(!visited[elem]){	
        this.dfsHelper(elem, visited);	
      }	
    }	
  }	
	
  doesPathExist(firstNode, secondNode){	
    let path = [];	
    let visited = this.createVisitedObject();	
    let q = [];	
    visited[firstNode] = true;	
    q.push(firstNode);	
    while(q.length){	
      let node = q.pop();	
      path.push(node);	
      let elements = this.AdjList.get(node);	
      if(elements.includes(secondNode)){	
        console.log(path.join('-&gt;'))	
        return true;	
      }else{	
        for(let elem of elements){	
          if(!visited[elem]){	
            visited[elem] = true;	
            q.unshift(elem);	
          }	
        }	
      }	
    }	
    return false;	
  }	
}

Vans，下一个。

8. 字典树： `Trie`

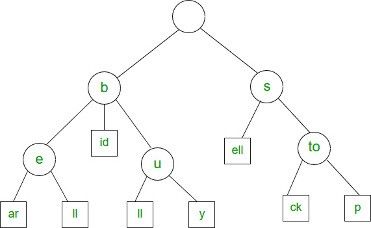
640?wx_fmt=png

Trie（通常发音为“try”）是针对特定类型的搜索而优化的树数据结构。当你想要获取部分值并返回一组可能的完整值时，可以使用 Trie。典型的例子是自动完成。

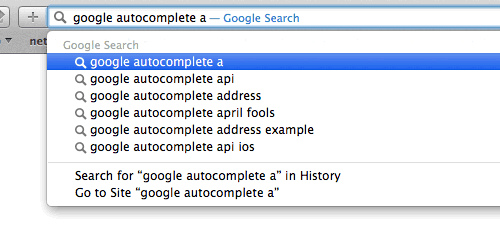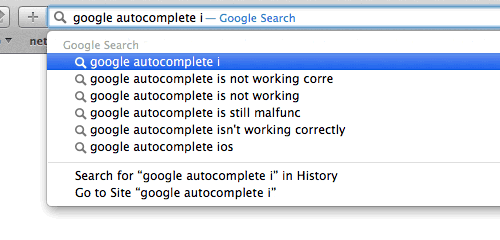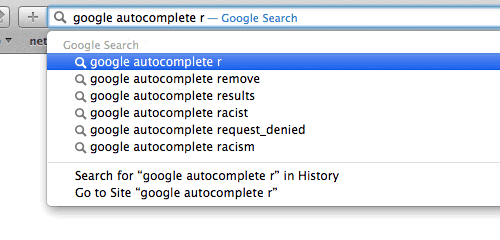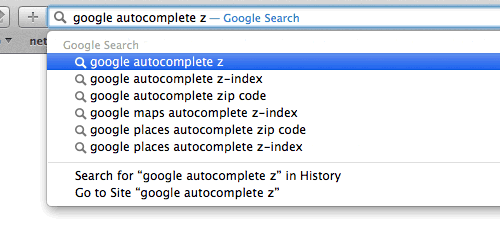
640?wx_fmt=gif

Trie，是一种搜索树，也称字典树或单词查找树，此外也称前缀树，因为某节点的后代存在共同的前缀。

它的特点：

key都为字符串，能做到高效查询和插入，时间复杂度为 O(k)，k为字符串长度
缺点是如果大量字符串没有共同前缀时很耗内存。
它的核心思想就是减少没必要的字符比较，使查询高效率。
即用空间换时间，再利用共同前缀来提高查询效率。

例如：搜索前缀“b”的匹配将返回6个值： be， bear， bell， bid， bull， buy。

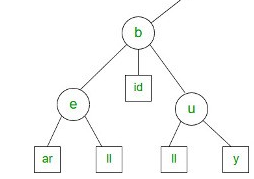
640?wx_fmt=png

搜索前缀“ be”的匹配将返回2个值： bear，bell

640?wx_fmt=png

8.1 字典树的应用

只要你想要将前缀与可能的完整值匹配，就可以使用 Trie。

现实中多运用在：

自动填充/预先输入
搜索
输入法选项
分类

也可以运用在：

IP地址检索
电话号码
以及更多...

8.2 字典树的实现

class PrefixTreeNode {	
  constructor(value) {	
    this.children = {};	
    this.endWord = null;	
    this.value = value;	
  }	
}	
class PrefixTree extends PrefixTreeNode {	
  constructor() {	
    super(null);	
  }	
  // 基础操作方法	
  // addWord(string) {}	
  // predictWord(string) {}	
  // logAllWords() {}	
}

1. `addWord`: 创建一个节点

addWord(string) {	
    const addWordHelper = (node, str) =&gt; {	
        if (!node.children[str[0]]) {	
            node.children[str[0]] = new PrefixTreeNode(str[0]);	
            if (str.length === 1) {	
                node.children[str[0]].endWord = 1;	
            } else if (str.length &gt; 1) {	
                addWordHelper(node.children[str[0]], str.slice(1));	
        }	
    };	
    addWordHelper(this, string);	
}

2. `predictWord`：预测单词

即：给定一个字符串，返回树中以该字符串开头的所有单词。

predictWord(string) {	
    let getRemainingTree = function(string, tree) {	
      let node = tree;	
      while (string) {	
        node = node.children[string[0]];	
        string = string.substr(1);	
      }	
      return node;	
    };	
	
    let allWords = [];	
	
    let allWordsHelper = function(stringSoFar, tree) {	
      for (let k in tree.children) {	
        const child = tree.children[k]	
        let newString = stringSoFar + child.value;	
        if (child.endWord) {	
          allWords.push(newString);	
        }	
        allWordsHelper(newString, child);	
      }	
    };	
	
    let remainingTree = getRemainingTree(string, this);	
    if (remainingTree) {	
      allWordsHelper(string, remainingTree);	
    }	
	
    return allWords;	
  }

3. `logAllWords`：打印所有的节点

  logAllWords() {	
    console.log('------ 所有在字典树中的节点 -----------')	
    console.log(this.predictWord(''));	
  }

logAllWords，通过在空字符串上调用 predictWord来打印 Trie中的所有节点。

9. 散列表（哈希表）： `HashTables`

使用哈希表可以进行非常快速的查找操作。但是，哈希表究竟是什么玩意儿？

很多语言的内置数据结构像 python中的字典， java中的 HashMap，都是基于哈希表实现。但哈希表究竟是啥？

9.1 哈希表是什么？

散列（hashing）是电脑科学中一种对资料的处理方法，通过某种特定的函数/算法（称为散列函数/算法）将要检索的项与用来检索的索引（称为散列，或者散列值）关联起来，生成一种便于搜索的数据结构（称为散列表）。也译为散列。旧译哈希（误以为是人名而采用了音译）。

它也常用作一种资讯安全的实作方法，由一串资料中经过散列算法（ Hashingalgorithms）计算出来的资料指纹（ data fingerprint），经常用来识别档案与资料是否有被窜改，以保证档案与资料确实是由原创者所提供。 —-Wikipedia

9.2 哈希表的构成

HashTables优化了键值对的存储。在最佳情况下，哈希表的插入，检索和删除是恒定时间。哈希表用于存储大量快速访问的信息，如密码。

哈希表可以概念化为一个数组，其中包含一系列存储在对象内部子数组中的元组：

{[[['a'，9]，['b'，88]]，[['e'，7]，['q'，8]]，[['j'，7]，['l '，8]]]};

外部数组有多个等于数组最大长度的桶（子数组）。
在桶内，元组或两个元素数组保持键值对。

9.3 哈希表的基础知识

这里我就尝试以大白话形式讲清楚基础的哈希表知识：

散列是一种用于从一组相似对象中唯一标识特定对象的技术。我们生活中如何使用散列的一些例子包括：

在大学中，每个学生都会被分配一个唯一的卷号，可用于检索有关它们的信息。
在图书馆中，每本书都被分配了一个唯一的编号，可用于确定有关图书的信息，例如图书馆中的确切位置或已发给图书的用户等。

在这两个例子中，学生和书籍都被分成了一个唯一的数字。

1. 思考一个问题

假设有一个对象，你想为其分配一个键以便于搜索。要存储键/值对，您可以使用一个简单的数组，如数据结构，其中键（整数）可以直接用作存储值的索引。

但是，如果密钥很大并且无法直接用作索引，此时就应该使用散列。

2, 一个哈希表的诞生

具体步骤如下：

在散列中，通过使用散列函数将大键转换为小键。
然后将这些值存储在称为哈希表的数据结构中。
散列的想法是在数组中统一分配条目（键/值对）。为每个元素分配一个键（转换键）。
通过使用该键，您可以在 O(1)时间内访问该元素。
使用密钥，算法（散列函数）计算一个索引，可以找到或插入条目的位置。

具体执行分两步：

通过使用散列函数将元素转换为整数。此元素可用作存储原始元素的索引，该元素属于哈希表。
该元素存储在哈希表中，可以使用散列键快速检索它。

hash = hashfunc（key）	
index = hash ％ array_size

在此方法中，散列与数组大小无关，然后通过使用运算符（％）将其缩减为索引（介于 0和 array_size之间的数字-1）。

3. 哈希函数

哈希函数是可用于将任意大小的数据集映射到固定大小的数据集的任何函数，该数据集属于散列表
哈希函数返回的值称为哈希值，哈希码，哈希值或简单哈希值。

要实现良好的散列机制，需要具有以下基本要求：

易于计算：它应该易于计算，并且不能成为算法本身。
统一分布：它应该在哈希表中提供统一分布，不应导致群集。
较少的冲突：当元素对映射到相同的哈希值时发生冲突。应该避免这些。

注意：无论散列函数有多健壮，都必然会发生冲突。因此，为了保持哈希表的性能，通过各种冲突解决技术来管理冲突是很重要的。

4. 良好的哈希函数

假设您必须使用散列技术 {“abcdef”，“bcdefa”，“cdefab”，“defabc”}等字符串存储在散列表中。

首先是建立索引：

a，b，c，d，e和 f的 ASCII值分别为 97,98,99,100,101和 102，总和为： 597
597不是素数，取其附近的素数 599，来减少索引不同字符串（冲突）的可能性。

哈希函数将为所有字符串计算相同的索引，并且字符串将以下格式存储在哈希表中。

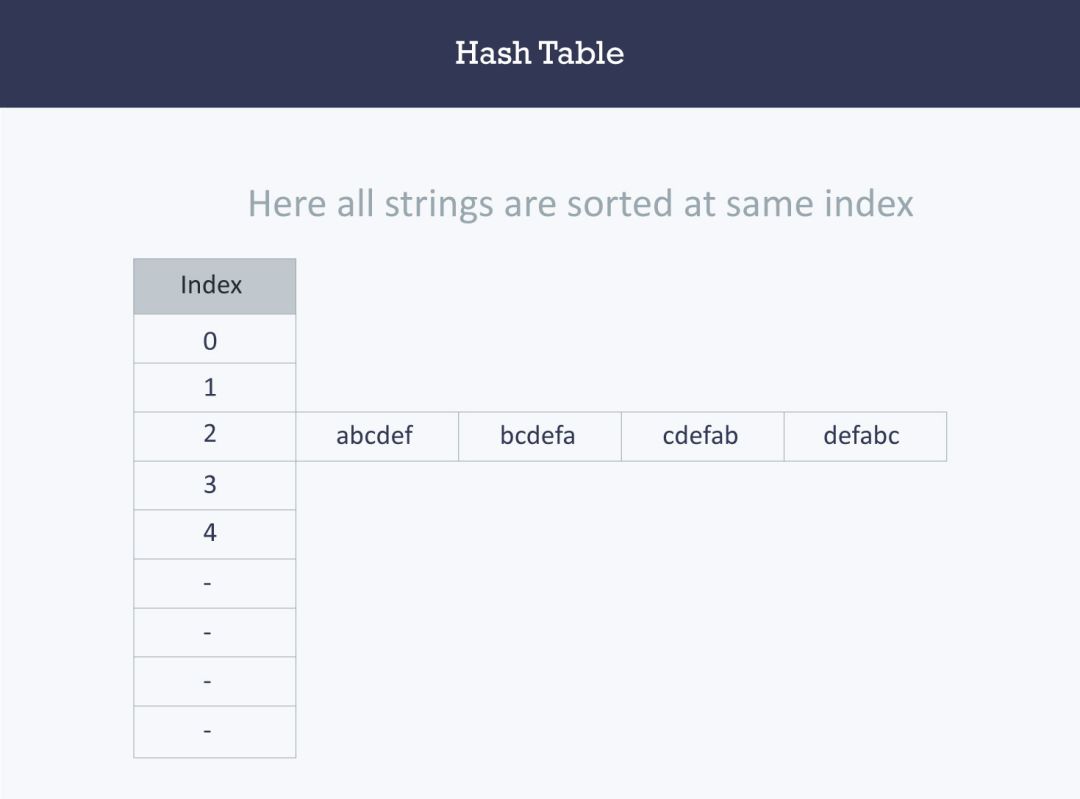
640?wx_fmt=png

由于所有字符串的索引都相同，此时所有字符串都在同一个“桶”中。

这里，访问特定字符串需要 O(n)时间（其中n是字符串数）。
这表明该哈希函数不是一个好的哈希函数。

如何优化这个哈希函数？

注意观察这些字符串的异同

{“abcdef”，“bcdefa”，“cdefab”，“defabc”}

都是由 a，b，c，d，e和 f组成
不同点在于组成顺序。

来尝试不同的哈希函数。

特定字符串的索引将等于字符的ASCII值之和乘以字符串中它们各自的顺序
之后将它与 2069（素数）取余。

字符串哈希函数索引

字符串	索引生成	计算值
abcdef	（97 1 + 98 2 + 99 3 + 100 4 + 101 5 + 102 6）％2069	38
bcdefa	（98 1 + 99 2 + 100 3 + 101 4 + 102 5 + 97 6）%2069	23
cdefab	（99 1 + 100 2 + 101 3 + 102 4 + 97 5 + 98 6）％2069	14
defabc	（100 1 + 101 2 + 102 3 + 97 4 + 98 5 + 99 6）%2069	11

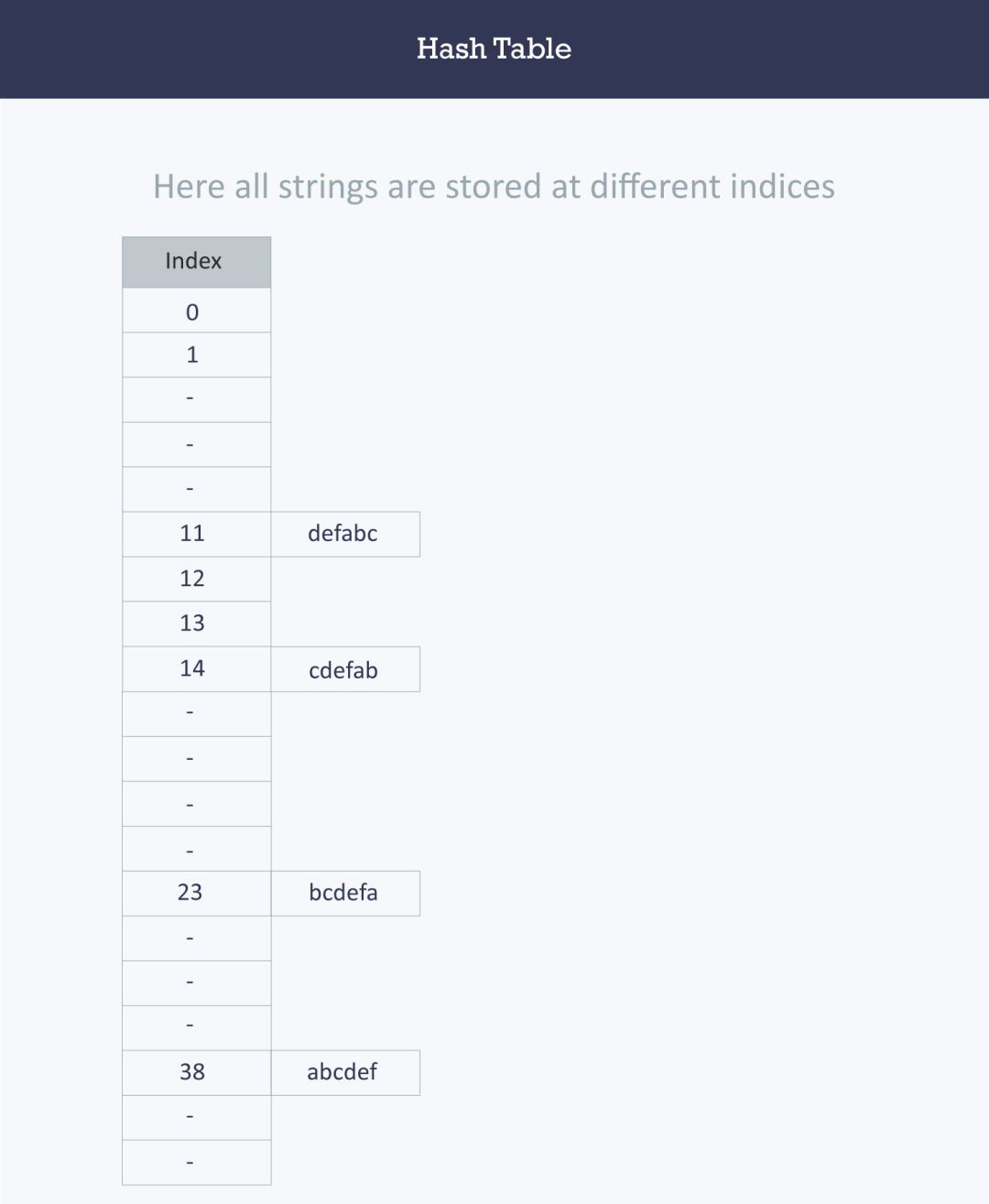
640?wx_fmt=png

在合理的假设下，在哈希表中搜索元素所需的平均时间应是O（1）。

9.4 哈希表的实现

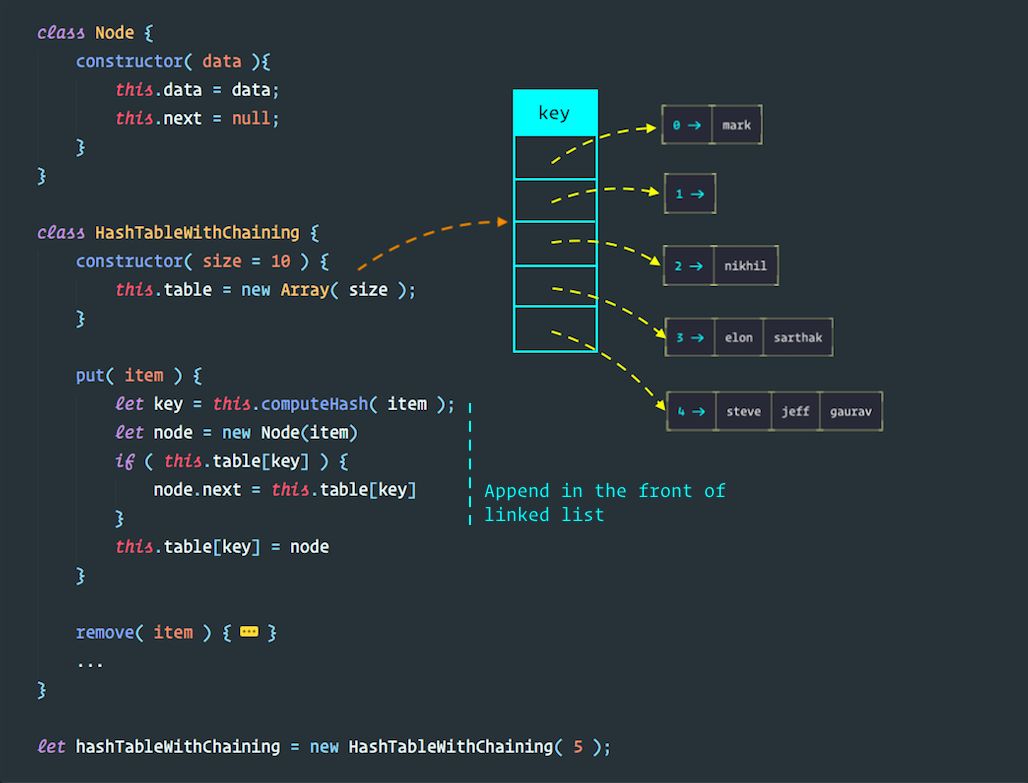
640?wx_fmt=png

class Node {	
    constructor( data ){	
        this.data = data;	
        this.next = null;	
    }	
}	
	
class HashTableWithChaining {	
    constructor( size = 10 ) {	
        this.table = new Array( size );	
    }	
	
    // 操作方法	
    // computeHash( string ) {...}	
    // ...	
}

1. 什么是数据结构？

1.1 为什么我们需要数据结构？

1.2 八大常见的数据结构

2.数组 - 知识补充

2.1 for...in为何这么慢？

3. 堆栈： Stack

3.1 堆栈的实现。

4. 队列： Queue

4.1 队列的实现

5. 链表： LinkedLists

5.1 单链表实现

5.2 双向链表实现

1. 双向链表的设计

2. 双向链表的操作方法

6. 树： Tree

6.1 树的分类

6.2 树的应用

6.3 二叉树： BinarySearchTree

6.4 二叉树的遍历

6.5 二叉树的实现

1. insertNode& insert：插入新子节点/节点

2. removeNode& remove：移除子节点/节点

3. findMinNode:获取子节点的最小值

4. searchNode & search：查找子节点/节点

7. 图： Graph

7.1 图的应用

7.2 图的构成

1. 图的基本元素

2. 符号和术语

3. 有向图与无向图

1. 有向图

2. 无向图

4. 加权图

5. 稀疏图与密集图

6. 循环

7.3 图的实现

1. addVertex：添加顶点

2. addEdge：添加边( Edge)

3. print：打印图( Graph)

测试一下

5. 广度优先算法实现

6. 深度优先算法实现

8. 字典树： Trie

8.1 字典树的应用

8.2 字典树的实现

1. addWord: 创建一个节点

2. predictWord：预测单词

3. logAllWords：打印所有的节点

9. 散列表（哈希表）： HashTables

9.1 哈希表是什么？

9.2 哈希表的构成

9.3 哈希表的基础知识

1. 思考一个问题

2, 一个哈希表的诞生

3. 哈希函数

4. 良好的哈希函数

9.4 哈希表的实现

2.1 `for...in`为何这么慢？

3. 堆栈： `Stack`

4. 队列： `Queue`

5. 链表： `LinkedLists`

6. 树： `Tree`

6.3 二叉树： `BinarySearchTree`

1. `insertNode`& `insert`：插入新子节点/节点

2. `removeNode`& `remove`：移除子节点/节点

3. `findMinNode`:获取子节点的最小值

4. `searchNode` & `search`：查找子节点/节点

7. 图： `Graph`

1. `addVertex`：添加顶点

2. `addEdge`：添加边( `Edge`)

3. `print`：打印图( `Graph`)

8. 字典树： `Trie`

1. `addWord`: 创建一个节点

2. `predictWord`：预测单词

3. `logAllWords`：打印所有的节点

9. 散列表（哈希表）： `HashTables`