使用MNIST数据集,这是一组由美国高中生和人口调查局员工手写的70000个数字的图片。
该数据集分成训练集(前6万张图片)和测试集(最后1万张图片)
1.训练二元分类器
先简化问题,只尝试识别一个数字,比如数字5
这里我们使用SGDClassifier分类器,你也可以使用RandomForestClassifier分类器
from sklearn.datasets import fetch_openml # 我的sklearn版本为1.0.2
from sklearn.linear_model import SGDClassifier
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# 下载mnist数据集,fetch_openml默认返回的是一个DataFrame,设置as_frame=False返回一个Bunch
# mnist.keys() 可查看所有的键
# data键,包含一个数组,每个实例为一行,每个特征为一列。
# target键,包含一个带有标记的数组
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
# 共有7万张图片,因为图片是28×28像素,所以每张图片有784个特征,每个特征代表了一个像素点的强度,从0(白色)到255(黑色)
x, y = mnist["data"], mnist["target"] # x.shape=(70000, 784),y.shape=(70000,)
y = y.astype(np.uint8) # 注意标签是字符,我们把y转换成整数
# 将数据集分为训练集和测试集
x_train, x_test, y_train, y_test = x[:60000], x[60000:], y[:60000], y[60000:]
# 我们可以看到第一张图片是5
some_digit = x[0]
some_digit_image = some_digit.reshape(28, 28) # 把长为784的一维数组转换成28x28的二维数组
# imshow用于生成图像,参数cmap用于设置图的Colormap,如果将当前图窗比作一幅简笔画,则cmap就代表颜料盘的配色
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off") # 关掉坐标轴
plt.show()
# 使用随机梯度下降(SGD)分类器,比如Scikit-Learn的SGDClassifier类
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
# max_iter最大迭代次数,random_state用于打乱数据,42表示一个随机数种子
sgd_clf = SGDClassifier(max_iter=1000, random_state=42)
sgd_clf.fit(x_train, y_train_5) # 在整个训练集上进行训练
# 模型预测
print(sgd_clf.predict([some_digit])) # 返回true2.性能测量
①交叉验证(Cross-validation)
交叉验证就是将拿到的训练数据,分为训练和验证集。首先用训练集对模型进行训练,再利用验证集来测试该模型。
n折交叉验证:将数据分成n份,其中1份作为验证集。然后经过n次测试,每次都更换不同的验证集。得到n个结果,取平均值作为最终结果。
from sklearn.model_selection import cross_val_score
# sgd_clf是分类器,x_train表示训练实例,y_train_5表示每个训练实例对应的标签,cv=3表示3-折交叉验证,accuracy表示使用准确率作为结果的度量指标
cross_val_score(sgd_clf, x_train, y_train_5, cv=3, scoring="accuracy") 结果
array([0.95035, 0.96035, 0.9604 ])但是,如果现在我有一个模型,对每张图片都判定为“非5” ,考虑到所有图片中有约10%的图片是5,这种模型训练下来的准确率也能达到90%左右,但是该模型永远正确无法识别“5‘。
这说明准确率通常无法成为分类器的首要性能指标,特别是当你处理有偏数据集时(即某些类比其他类更为频繁)。
②混淆矩阵
评估分类器性能的更好方法是混淆矩阵,其总体思路就是统计A被识别成B的次数。
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
# 获取每次预测的结果,cv=3表示3-折交叉验证
y_train_pred = cross_val_predict(sgd_clf, x_train, y_train_5, cv=3)
# 构造混淆矩阵,y_train_5包含目标类别,y_train_pred包含对应的预测类别
confusion_matrix(y_train_5, y_train_pred)
结果
array([[53892, 687],
[ 1891, 3530]])
# 真负类(TN) 假正类(FP)
# 假负类(FN) 真正类(TP)
# 真负类: 53892张“非5”图片被正确识别
# 假正类: 687张“非5”图片被错误地识别为“5”
# 假负类: 1891张“5”图片被错误地识别为“非5”
# 真正类:3530张“5”图片被正确识别一个完美的分类器,它的副对角线的值都为0
# 我们可以假设我们都识别对了,打印出来看看
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions)
# 结果
array([[54579, 0],
[ 0, 5421]])③精度和召回率
精度 (Precision)=TP/(TP+FP) :你认为的该类样本,有多少猜对了(猜的精确性如何)。
召回率 (Recall)=TP/(TP+FN):该类样本有多少被找出来了(召回了多少)。
F1分数是精度和召回率的谐波平均值,正常的平均值平等对待所有的值,而谐波平均值会给予低值更高的权重。因此,只有当召回率和精度都很高时,分类器才能得到较高的F1分数。

from sklearn.metrics import precision_score, recall_score, f1_score
precision_score(y_train_5, y_train_pred) # 精度,0.8370879772350012
recall_score(y_train_5, y_train_pred) # 召回率,0.6511713705958311
f1_score(y_train_5, y_train_pred) # f1分数 F1分数对那些具有相近的精度和召回率的分类器更为有利。
这不一定能一直符合你的期望:在某些情况下,你关心的是精度,而另一些情况下,你关心的是召回率。 例如,
①假设你训练一个分类器来检测儿童可以放心观看的视频,那么你可能更青睐那种拦截了很多好视频(低召回率),但是保留下来的视频都是安全(高精度)的分类器。
②如果你训练一个分类器通过图像监控来检测小偷:你大概可以接受精度只有30%,但召回率能达到99%(当然,安保人员会收到一些错误的警报,但是几乎所有的窃贼都在劫难逃)。
精度/召回率权衡:关键要调整阈值(SGDClassifier分类器使用的阈值是0。)
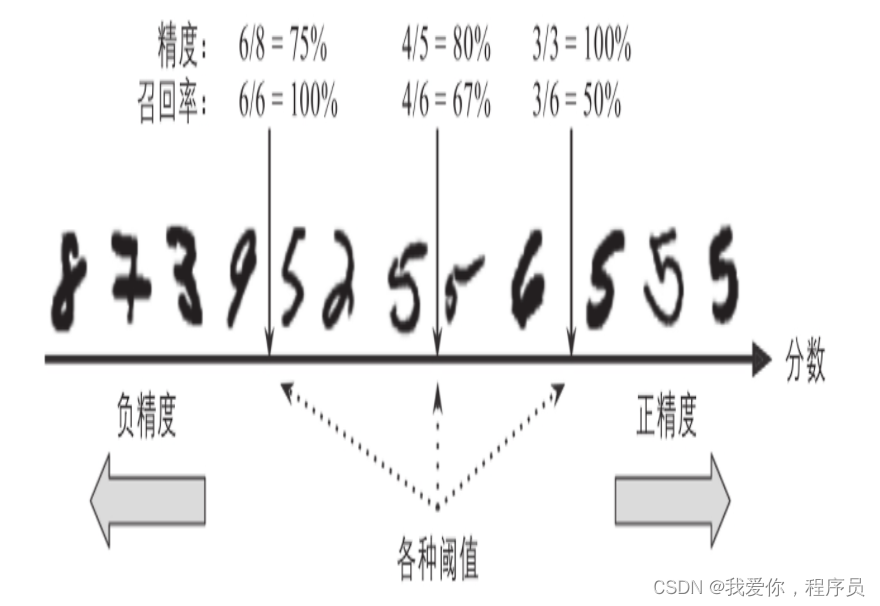
怎么理解这幅图:以中间阈值为例,就预测结果而言,右边图片我全部预测为“5”,5个猜对4个,精度:4/5。就整个样本而言,共有6个“5”,我只找到4个“5”,召回率:4/6。
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt
import numpy as np
# 使用cross_val_predict函数获取训练集中所有实例的决策分数
y_scores = cross_val_predict(sgd_clf, x_train, y_train_5, cv=3, method="decision_function")
# 使用precision_recall_curve函数来计算所有可能的阈值的精度和召回率
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
# 使用Matplotlib绘制精度和召回率相对于阈值的函数图
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2) # b--的b表示蓝色,--表示虚线,下面的g--同理
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.legend(loc="center right", fontsize=16) # 设置图例的位置和大小
plt.xlabel("Threshold", fontsize=16) # x轴标签
plt.grid(True) # 显示网格线
plt.axis([-50000, 50000, 0, 1]) # 设置x轴的范围和y轴的范围
# 假设你决定将精度设为90%
# np.argmax返回数组中最大值的第一个索引,这种情况下,它返回第一个True值
recall_90_precision = recalls[np.argmax(precisions >= 0.90)] # 返回精度90%的召回率
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)] # 返回精度90%时候的阈值
plt.figure(figsize=(8, 4)) # 创建一个绘图对象,设置宽高
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:") # 点线
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:") # 点线
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")# 点线
plt.plot([threshold_90_precision], [0.9], "ro") # 阈值为threshold_90_precision,和精度线的交点
plt.plot([threshold_90_precision], [recall_90_precision], "ro") # 阈值为threshold_90_precision,和召回率线的交点
plt.show()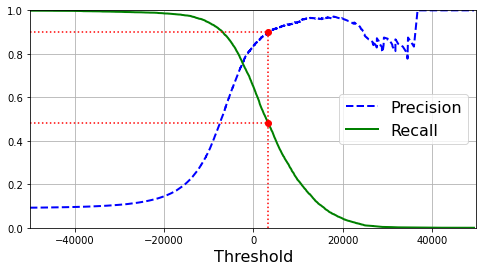
我们利用threshold_90_precision这个阈值再来看看精度和召回率
y_train_pred_90 = (y_scores >= threshold_90_precision)
precision_score(y_train_5, y_train_pred_90) # 0.9000345901072293
recall_score(y_train_5, y_train_pred_90) # 0.4799852425751706④ROC曲线
ROC(Receiver Operating Characteristic): 受试者工作特征
该曲线绘制的是灵敏度(Specificity)和 假正类率(FPR)
灵敏度 = 召回率(TPR),假正类率 = 1-特异度(Sensitivity) = 1 - 真负类率(TNR)
召回率: 被正确分为正类的正类实例比率。
假正类率:被错误分为正类的负类实例比率。
真负类率/特异度:被正确分类为负类的负类实例比率。
from sklearn.metrics import roc_curve
# 使用roc_curve函数计算多种阈值的TPR(真正类率)和FPR(假正类率)
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # 画对角线,虚线
plt.axis([0, 1, 0, 1]) # 坐标轴范围
plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # x轴标签
plt.ylabel('True Positive Rate (Recall)', fontsize=16) # y轴标签
plt.grid(True) # 网格线
plt.figure(figsize=(8, 6)) # 设置图片宽高
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)] # 精度90%时的召回率对应的假正类率
plt.plot([fpr_90], [recall_90_precision], "ro") # 精度90%时的召回率对应的那个点
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:") # 那个点到x轴的虚线
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:") # 那个点到y轴的虚线
plt.show()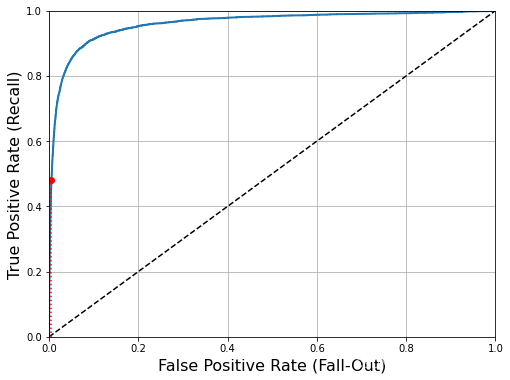
虚线表示纯随机分类器的ROC曲线、一个优秀的分类器应该离这条线越远越好(向左上角) 。
⑤ROC AUC(Area Under Curve) 曲线下面积
完美的分类器的ROC AUC等于1,而纯随机分类器的ROC AUC等于0.5。
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)⑥ROC曲线与精度/召回率(PR)曲线的抉择
当正类非常少见或者你更关注假正类而不是假负类时,应该选择PR曲线,反之则是ROC曲线。
例如,看前面的ROC曲线图,你可能会觉得分类器真不错。但这主要是因为跟负类(非5)相比,正类(数字5)的数量真的很少。相比之下,PR曲线清楚地说明分类器还有改进的空间(曲线还可以更接近左上角)。
3.多类分类器
二元分类器只能区分两个类,而多类分类器可以区分两个以上的类。
随机森林分类器和朴素贝叶斯分类器可以直接处理多个类。
支持向量机分类器和线性分类器则是严格的二元分类器。
要创建一个系统将数字图片分为10类(从0到9)
①一对剩余(OvR)策略:训练10个二元分类器,每个数字一个(0-检测器、1-检测器、2-检测器,以此类推)。当你需要对一张图片进行检测分类时,获取每个分类器的决策分数,哪个分类器给分最高,就将其分为哪个类。
②一对一(OvO)策略:为每一对数字训练一个二元分类器(一个区分0和1,一个区分0和2,一个区分1和2,以此类推)。如果存在N个类别,那么这需要训练N×(N-1)/2个分类器。
对该问题而言,当需要对一张图片进行分类时,你需要运行45个分类器来对图片进行分类,最后看哪个类获胜最多。
优点:每个分类器只需要用到部分训练集对其必须区分的两个类进行训练。
Scikit-Learn会根据情况自动运行OvR或者OvO。
(1)使用sklearn.svm.SVC类(Support Vector Classification 支持向量机用于分类)
from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(x_train, y_train)
svm_clf.predict([some_digit])Scikit-Learn实际上训练了45个二元分类器,获得它们对图片的决策分数,然后选择了分数最高的类。
如果想要强制Scikit-Learn使用OvO或者OvR策略,可以使用OneVsOneClassifier或OneVsRestClassifier类。
from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))
ovr_clf.fit(x_train[:1000], y_train[:1000])
ovr_clf.predict([some_digit])目标类的列表会存储在classes_属性中,在本例里,classes_数组中每个类的索引正好对应其类本身。
svm_clf.classes_(2)训练SGDClassifier
sgd_clf.fit(x_train, y_train)
sgd_clf.predict([some_digit])
cross_val_score(sgd_clf, x_train, y_train, cv=3, scoring="accuracy") # 交叉验证优化:归一化
StandardScaler():去均值和方差归一化
归一化:保证每个维度数据方差为1,均值为0,加快了梯度下降求最优解的速度,提高精度
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train.astype(np.float64))
cross_val_score(sgd_clf, x_train_scaled, y_train, cv=3, scoring="accuracy")4.改进模型---误差分析
首先看看混淆矩阵
y_train_pred = cross_val_predict(sgd_clf, x_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
plt.matshow(conf_mx, cmap=plt.cm.gray) # 绘制矩阵
plt.show()
大多数图片都在主对角线上,这说明它们被正确分类。
数字5看起来比其他数字稍暗,可能是因为数据集中数字5的图片较少,也可能是因为分类器在数字5上的执行效果不如在其他数字上好。
让我们把焦点放在错误上
row_sums = conf_mx.sum(axis=1, keepdims=True) # axis=1表示以竖轴为基准,一行的数求和,keepdims=True表示保持二维特性
norm_conf_mx = conf_mx / row_sums # 将混淆矩阵中的每个值除以相应类中的图片数量
np.fill_diagonal(norm_conf_mx, 0) # 矩阵正对角线都填充为0,也就是涂得最黑
plt.matshow(norm_conf_mx, cmap=plt.cm.gray) # 绘制矩阵
plt.show()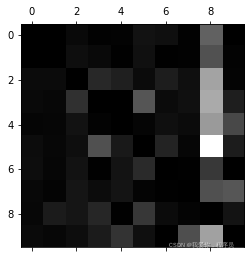
每行代表实际类,而每列表示预测类。
第8列看起来非常亮,说明有许多图片被错误地分类为数字8了。
然而,第8行不那么差,告诉你实际上数字8被正确分类为数字8。
因此,你的精力可以花在改进数字8的分类错误上。
例如,可以试着收集更多看起来像数字8的训练数据去训练。或者对图片进行预处理(例如Scikit-Image、Pillow或OpenCV)让某些模式更为突出,比如闭环(8有两个,6有一个,5没有)。
5.多标签分类
在某些情况下,你希望分类器为每个实例输出多个类。
例如,人脸识别的分类器:如果在一张照片里识别出多个人,应该为识别出来的每个人都附上一个标签。举个例子,分类器经过训练能够识别三张脸—张三、李四和王五,那么当看它到张三和王五的照片时,它应该输出[1,0,1](“是张三,不是李四,是王五”)
下面看一个实例
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7) # 打标签:该数字是不是大于7
y_train_odd = (y_train % 2 == 1) # 打标签:该数字是不是奇数
y_multilabel = np.c_[y_train_large, y_train_odd] # np.c_用于拼接两个矩阵
knn_clf = KNeighborsClassifier() # 该分类器支持多标签分类
knn_clf.fit(x_train, y_multilabel) # 训练
knn_clf.predict([some_digit]) # 返回array([[False, True]]),数字5确实不大于7(False),为奇数(True)评估多标签分类器
测量每个标签的F1分数,简单地计算平均分数
y_train_knn_pred = cross_val_predict(knn_clf, x_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")这里假设所有的标签都同等重要,但实际可能不是这样。
一个简单的办法:给每个标签设置一个权重(也就是具有该目标标签的实例的数量)。
为此,只需要在上面的代码中设置average="weighted"即可。
6.多输出分类
多输出分类:多标签分类的泛化,其标签也可以是多类的(比如它可以有两个以上可能的值)
举例:构建一个系统去除图片中的噪声。
这个分类器的输出是多个标签(一个像素点一个标签),每个标签可以有多个值(像素强度范围为0到225)
# 为MNIST图片的像素强度增加噪声(因为原来图片是干净的)
noise = np.random.randint(0, 100, (len(x_train), 784))
x_train_mod = x_train + noise
noise = np.random.randint(0, 100, (len(x_test), 784))
x_test_mod = x_test + noise
# 目标是将图片还原为原始图片,所以标签是原来图片的数据
y_train_mod = x_train
y_test_mod = x_test训练之前看看训练的目标图片,和对应的标签 (清洗后的图片)
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.binary, interpolation="nearest")
plt.axis("off")
index = 0 # 查看第一张目标图片,和它的标签(清洗后的图片)
plt.subplot(121); plot_digit(x_test_mod[index]) # 1代表行,2代表列,所以一共有2个图,1代表此时绘制第以个图
plt.subplot(122); plot_digit(y_test_mod[index]) # 2代表此时绘制第二个图
plt.show()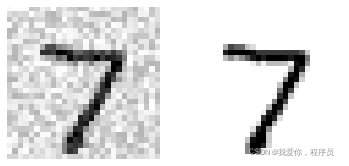
knn_clf.fit(x_train_mod, y_train_mod) # 根据训练集进行训练
clean_digit = knn_clf.predict([x_test_mod[index]]) # 对输入的有噪声图片进行处理
plot_digit(clean_digit) # 查看去除噪声的图片