从np random normal 到正态分布的拟合

先看伟大的高斯分布（Gaussian Distribution）的概率密度函数（probability density function）：

采样（sampling）

# 从某一分布（由均值和标准差标识）中获得样本mu, sigma =0,.1s = np.random.normal(loc=mu, scale=sigma, size=1000)

• 1
• 2
• 3

也可使用scipy库中的相关api（这里的类与函数更符合数理统计中的直觉）：

import scipy.stats asstmu, sigma =0,.1s =st.norm(mu, sigma).rvs(1000)

• 1
• 2
• 3

校验均值和方差：

>>>abs(mu < np.mean(s)) <.01True>>>abs(sigma-np.std(s, ddof=1)) <.01True# ddof，delta degrees of freedom，表示自由度# 一般取1，表示无偏估计，

• 1
• 2
• 3
• 4
• 5
• 6

拟合

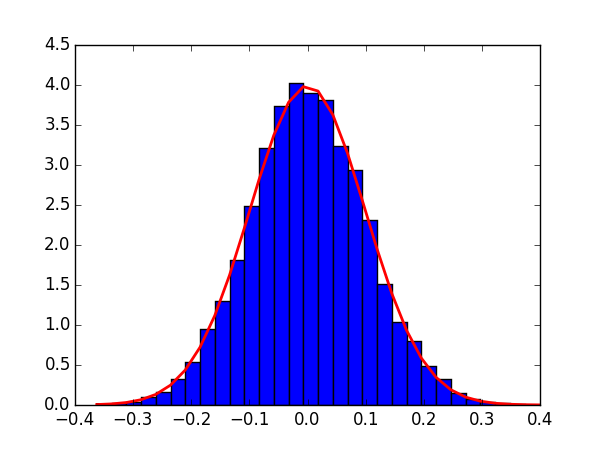
我们看使用matplotlib.pyplot便捷而强大的语法如何进行高斯分布的拟合：

import matplotlib.pyplot as pltcount, bins, _ = plt.hist(s,30, normed=True)# normed是进行拟合的关键# count统计某一bin出现的次数，在Normed为True时，可能其值会略有不同plt.plot(bins,1./(np.sqrt(2*np.pi)*sigma)*np.exp(-(bins-mu)**2/(2*sigma**2), lw=2, c='r')plt.show()

• 1
• 2
• 3
• 4
• 5
• 6

或者：

s_fit = np.linspace(s.min(), s.max())plt.plot(s_fit,st.norm(mu, sigma).pdf(s_fit), lw=2, c='r')

• 1
• 2