一、算法要求
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为c。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
1. 思路
有n种可选物品1,…,n ,放入容量为c的背包内,使装入的物品具有最大效益。
n :物品个数
c :背包容量
p1,p2, …, pn:个体物品效益值
w1,w2, …,wn:个体物品容量
0-1背包问题的解法:物品1,…,n的一种放法(x1, ···,xn的0/1赋值),使得效益值最大。
假定背包容量不足以装入所有物品:面临选择
优化原理:无论优化解是否放物品1,优化解对物品2,…,n的放法,相对剩余背包容量,也是优化解。2. 示例
假设:n=5,c=10
p=[6,3,5,4,6]
w=[2,2,6,5,4]
(1,1,0,0,1)为其优化解,即放物品1,2,5 。物品1占背包容量2,剩下容量为8。
考虑子问题:n=4,c=8,物品为2,3,4,5
(1,0,0,1),即放物品2和5,是子问题的优化解,背包问题满足优化原理。
二、完整代码
1. 主文件
main.cpp:
#include"Improve1.h"intmain(){//初始化控制台Console();//核心算法CoreAlgorithm();// 输出
cout<<"\nThe maximum total value of the items in the backpack is:"<< m[1][capacityPack]<< endl;
cout<<"The selected item situation is:";for(int i=1; i<= numItem; i++)
cout<< x[i]<<" ";
cout<< endl;return0;}2. 头文件
Improve1.h:
#pragmaonce#ifndef__IMPROVE1__#define__IMPROVE1__#include<iostream>#include<iomanip>#include<cstdio>#include<algorithm>
using namespace std;/*n :物品个数
*c :背包容量
*p1,p2, …, pn:个体物品效益值
*w1,w2, …,wn:个体物品容量*/int numItem=5,
capacityPack=10;int weightItem[]={0,2,2,6,5,4},//从第一序列开始
valueItem[]={0,6,3,5,4,6};int* x;// 物品是否被放入背包int** m;// 最大价值// 用户输入voidConsole(){
cout<<"The following are the default items’ quantity, value and weight and backpack capacity: \n"<<"\n#Number of items: "<< numItem<<"\n#Number of backpacks: "<< capacityPack;
cout<<"\n#Corresponding weight: ";for(int i=1; i< numItem+1; i++)
cout<<setw(3)<< weightItem[i];
cout<<"\n#Corresponding value: ";for(int i=1; i< numItem+1; i++)
cout<<setw(3)<< valueItem[i];
x= newint[numItem+1];
m= newint*[numItem+1];for(int i=0; i<= numItem; i++){
m[i]= newint[capacityPack+1];memset(m[i],0,sizeof(int)*(capacityPack+1));// 将表m所有元素设为0}
cout<< endl;}//核心算法voidCoreAlgorithm(){//Knapsack最大价值表int jMax=min(weightItem[numItem]-1, capacityPack);// 避免存在单个重量超出背包容量的物品使数组m越界for(int j=0; j<= jMax; j++)// 以下两个for循环是最大价值表m的最后一行
m[numItem][j]=0;for(int j= weightItem[numItem]; j<= capacityPack; j++)
m[numItem][j]= valueItem[numItem];for(int i= numItem-1; i>1; i--){// 以下是表m最后一行以上的部分
jMax=min(weightItem[i]-1, capacityPack);for(int j=0; j<= jMax; j++)// 背包容量<物品重量,即装不下;将m[i+1][j](下一行同列)的值赋给m[i][j]
m[i][j]= m[i+1][j];for(int j= weightItem[i]; j<= capacityPack; j++)// 背包容量>=物品重量,即可以装下;// 放:m[i][j]=m[i + 1][j - w[i]] + v[i]// 不放:m[i][j]=m[i + 1][j]// 哪个价值大,就采取哪种方式
m[i][j]=max(m[i+1][j], m[i+1][j- weightItem[i]]+ valueItem[i]);}
m[1][capacityPack]= m[2][capacityPack];if(capacityPack>= weightItem[1])
m[1][capacityPack]=max(m[1][capacityPack], m[2][capacityPack- weightItem[1]]+ valueItem[1]);//Traceback将最优解存入数组int cTemp= capacityPack;// 临时背包容量for(int i=1; i< numItem; i++){if(m[i][cTemp]== m[i+1][cTemp])
x[i]=0;// 价值相等,说明没有放入这个物品,0else{
x[i]=1;// 价值不相等,说明放入了这个物品,1
cTemp-= weightItem[i];// 放入了一个物品,背包剩余容量为原容量-物品重量}}
x[numItem]=(m[numItem][capacityPack])?1:0;// 最后一个物品,非0为true放入,0为false不放入}#endif3. 效果展示
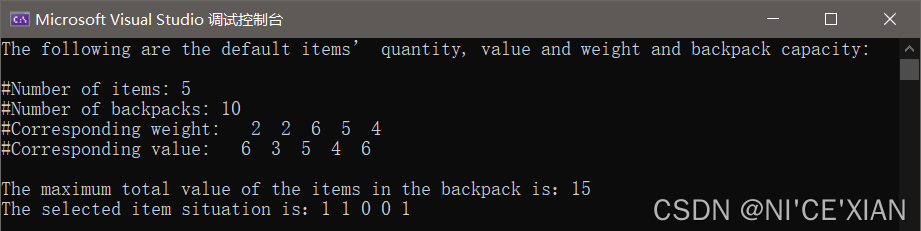
三、补充
优化值间的递归式:
虽然不知道优化解是否放物品1,但从优化原理能建立优化值间的递归式:
设f(i, y)为以背包容量y,放物品i,…,n,得到的优化效益值,以下递归关系成立:
f(1,c)=max{f(2,c), f(2,c-w1)+p1} 不放物品1、放物品1
先求子问题的优化值(递归),再从2种可能性中求出最优的。须对任意给定容量y,任意i,…,n 种物品求解子问题。
举例:
n=3, c=116
w=[100,14,10]
p=[20,18,15]
放进物品1(x1 = 1),背包容量还剩r=16, [x2,x3]= [1,0] 为子问题的优化解,值为18,总效益值为20+18=38
不放物品1(x1= 0)则对于剩下的两种物品而言,容量限制条件为116,[1,1]为子问题优化解,值为33。
前者效益值为38,后者为33;
所以优化解为[1,1,0], 优化值为max{38,33}=38。- 算法复杂度分析:
(1)时间复杂度:算法中有主要的是两层嵌套的for循环,其时间复杂度为O(n×w)。
(2)空间复杂度:由于二维数组c[n][w],所以空间复杂度为O(n×w)。 - 算法优化拓展:
首先有一个主循环i=1,2,…,N,每次算出来二维数组c[i][0~w]的所有值。那么,如果只用一个数组 dp[0~w],能不能保证第i次循环结束后dp[i]中表示的就是我们定义的状态 c[i][j]呢?
c[i]]由c[i-1][i]和c[i-1] [j-w[i]]两个子问题递推而来,能否保证在递推 c[i][i]时(也即在第i次主循环中递推 dp[j]时)能够得到c[i-1][j]和c[i-1][j-w[i]]的值呢﹖事实上,这要求在每次主循环中以j=w,w-1,…,1,0的顺序倒推dp[j],这样才能保证递推 dp[j]时dp[j-c[i]]保存的是状态c[i-1][j-w[i]]的值。
伪代码如下:
for i=1..nfor j=w..0
dp[j]=max{dp[j],dp[j-w[i]]+v[i]};其中,dp[j]=max {dp[j],dp[j-w[i]]}就相当于转移方程c[i][j]-max {c[i-1][j],c[i-1][j-w[i]]},
因为这里的dp[j-w[i]] 就相当于原来的c[i-1][j-w[i]]。文档供本人学习笔记使用,仅供参考。