目录
0.层次聚类的概念
层次聚类和k-means一样都是很常用的聚类方法。层次聚类是对群体的划分，最终将样本划分为树状的结构。他的基本思路是每个样本先自成一类，然后按照某种规则进行合并，直到只有一类或者某一类的样本只有一个点。层次聚类又分为自底而上的聚合层次聚类和自顶而下的分裂层次聚类。
参考链接：
关于层次聚类算法的python实现 - 简书 (jianshu.com)
https://www.jianshu.com/p/916aab25cda7
0.1 聚合层次聚类
每一个点初始为1类，得到N(样本点个数)类，计算每一类之间的距离，计算方法有很多，具体可以参考距离的计算方法。聚合层次聚类方法的终止条件是所有样本点都处于同一类了，或者两类之间的距离超过设置的某个阈值。大多数层次聚类都是聚合层次聚类。
0.2 分裂层次聚类
和聚合层次聚类是反着的，属于自上而下的一种聚类方法。刚开始的时候所有的样本点都位于同一类，然后一步步划分，终止条件是所有的样本点都位于单独的一类，或者两类之间的距离超过设置的某个阈值。
下面这个图可以比较好的说明这个过程：
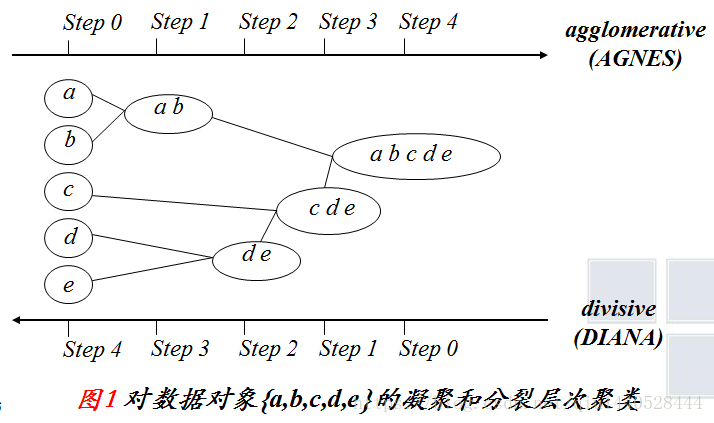
层次聚类的两种方法
1.凝聚层次聚类算法步骤
1.1 算法过程
参考链接：
(2条消息) 层次聚类算法的原理及python实现_听了个听儿-CSDN博客_层次聚类pythonhttps://blog.csdn.net/u012328476/article/details/78978113层次聚类的合并算法通过计算两类数据点间的相似性，对所有数据点中最为相似的两个数据点进行组合，并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性，距离越小，相似度越高。并将距离最近的两个数据点或类别进行组合，生成聚类树。合并过程如下：
我们可以获得一个N*N的距离矩阵 X，其中X[i,j]表示i和j的距离，称为数据点与数据点之间的距离。记每一个数据点为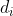
,将距离最小的数据点进行合并，得到一个组合数据点，记为 G
数据点与组合数据点之间的距离: 当计算G 和的距离时，需要计算和G中每一个点的距离。
组合数据点与组合数据点之间的距离：主要有Single Linkage，Complete Linkage和Average Linkage、Ward linkage 四种。这四种算法介绍如下：
1.Single Linkage
Single Linkage的计算方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
2. Complete Linkage
Complete Linkage的计算方法与Single Linkage相反，将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反，两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
3. Average Linkage
Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大，但结果比前两种方法更合理。
1）N个样本单独成类，G1(0)、G2(0)、G3(0)、……、GN(0)，0代表初始状态。
2）更新距离矩阵D(n)，找出D(n)中最小值，把对应的两类合并为1类。
3）更新距离矩阵D(n+1)，重复步骤2-3。
当两类之间的最小距离小于给定的阈值或者所有样本都单独成类的时候，结束算法。
4.Ward linkage
参考链接
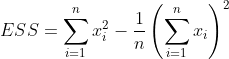
1.2算法案例
参考链接
原理+代码｜详解层次聚类及Python实现 - 云+社区 - 腾讯云 (tencent.com)https://cloud.tencent.com/developer/article/1756976
使用一份公开的城市经济数据集，参数如下：
- AREA：城市名称
- Gross：总体经济情况指数
- Avg：平均经济情况指数
import matplotlib.pyplot as plt
import pandas as pd
import scipy.cluster.hierarchy as sch
plt.rc('font', **{'family': 'Microsoft YaHei, SimHei'}) # 设置中文字体的支持
plt.rcParams['axes.unicode_minus'] = False # 使坐标轴刻度表签正常显示正负号,解决保存图像是负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 图中文字体设置为黑体
plt.rcParams['axes.unicode_minus'] = False # 负值显示
df = pd.read_csv('城市经济.csv', encoding='GBK', engine='python')#解决中文乱码
name = df['AREA'].values.reshape(df['AREA'].values.shape[0], 1)#提取数据并转置
datax = df['Gross'].values.reshape(df['Gross'].values.shape[0], 1)
datay = df['Avg'].values.reshape(df['Avg'].values.shape[0], 1)
fig1 = plt.figure(figsize=(6, 6)) # 新建画布
ax = fig1.add_subplot(1, 1, 1)
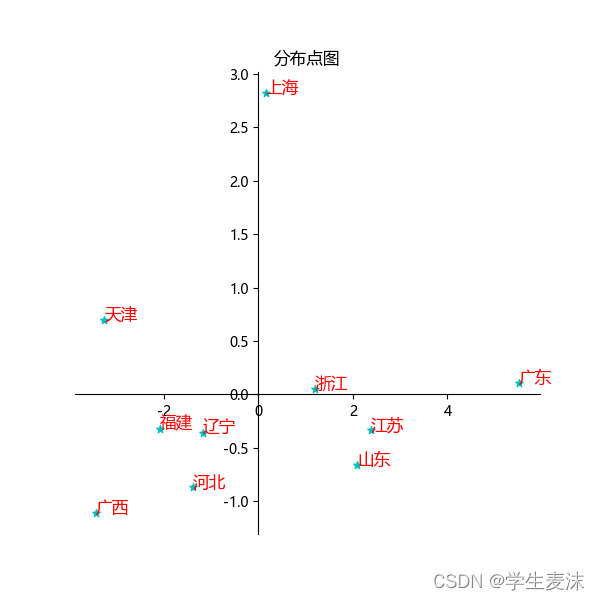
ax.scatter(datax, datay, marker='*', color='c', label='3', s=30) # 绘制散点图
ax.set_title("分布点图")
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none') # 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边
ax.spines['bottom'].set_position(('data', 0)) # 指定 data 设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
ax.spines['left'].set_position(('data', 0))
# 为点添加标签
for i in range(10):
ax.text(datax[i], datay[i], df['AREA'].values[i], fontsize=12, color="r", style="italic")
plt.show()
plt.close()
# 生成点与点之间的距离矩阵, 这里用的欧氏距离: euclidean
# X：根据什么来聚类，这里结合总体情况 Gross 与平均情况 Avg 两者
disMat = sch.distance.pdist(X=df[['Gross', 'Avg']], metric='euclidean')
# 进行层次聚类: 计算距离的方法使用 ward 法
Z = sch.linkage(disMat, method='ward')
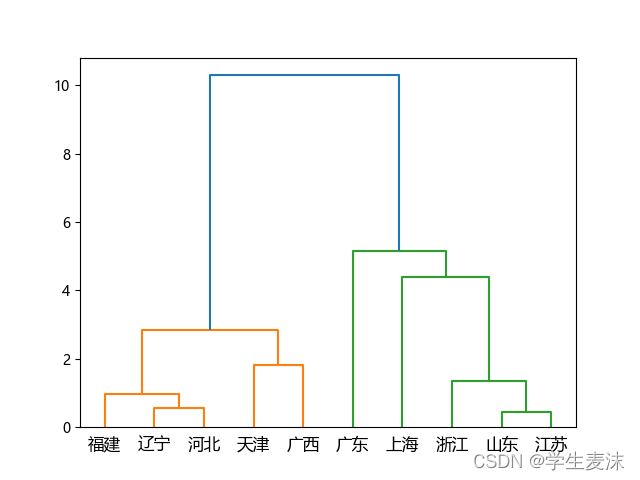
# 将层级聚类结果以树状图表示出来并保存
# 需要手动添加标签。
# P = sch.dendrogram(Z, labels=name)
P = sch.dendrogram(Z, labels=df.AREA.tolist())
plt.savefig('层次聚类.png')
